Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.
Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.

La contrarellotge s'ha acabat amb èxit!
Enhorabona al guanyador de la prova oficial: Gauss!
Atenció: el problema 15 ha quedat anul·lat degut a un error en les opcions (cap opció contenia la resposta correcta).
Esperem que el concurs també haja servit de pràctica als estudiants de 3r i 4t d'ESO: la setmana que ve serà la vostra prova oficial!
Problema 1
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Quina peça dels escacs tindrà accés a més caselles si la situem a una de les caselles centrals del tauler?

La dama es pot moure a un total de $27$ caselles:

Aquestes caselles inclouen totes les caselles accessibles per l'alfil, la torre i el rei. D'altra banda, el cavall només pot accedir a $8$ caselles.
Problema 2
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Situem un cavall d'escacs a una cantonada d'un tauler d'escacs de $3\times3$. Quants salts de cavall necessitem per visitar les $8$ caselles restants?

El cavall mai podrà visitar la casella del centre:

Si situem un cavall al centre, aquest no pots accedir a cap altra casella. Per tant, des de cap altra casella tampoc es pot accedir al centre.
Problema 3
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Problema 4
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Problema 5
3 punts
1 min
30 s
3 punts
•
1 min
30 s
A cada casella d'un tauler d'escacs situem el número $1$ o el número $-1$, de manera que es compleixen aquestes condicions:
- El producte dels números de cada fila és negatiu.
- El producte dels números de cada columna és negatiu.
Quin és el mínim nombre de $-1$ que hem de col·locar?
Problema 6
4 punts
3 min
4 punts
•
3 min
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 7
4 punts
3 min
4 punts
•
3 min
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 8
4 punts
3 min
4 punts
•
3 min
Quin és el mínim nombre d'alfils que hem de col·locar a un tauler d'escacs de manera que:
- Cap parella d'alfils s'amenacen entre ells.
- Qualsevol casella del tauler és accessible per algun alfil.
Per exemple, amb $8$ torres ho podríem fer:
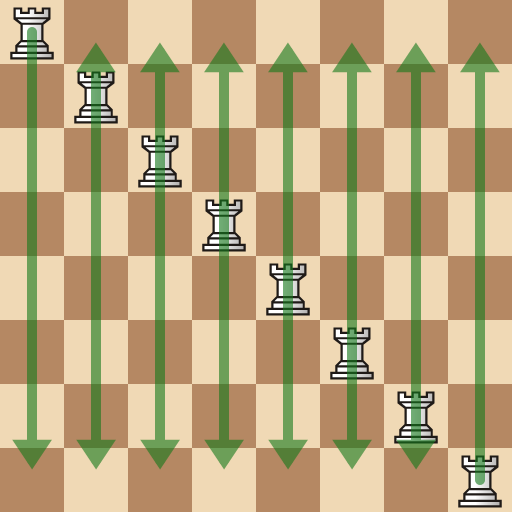
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 9
4 punts
3 min
4 punts
•
3 min
Els cercles petits de la figura tenen radi $1$. El cercle petit del centre és tangent als sis que té al voltant, els quals són tangents al cercle gran:
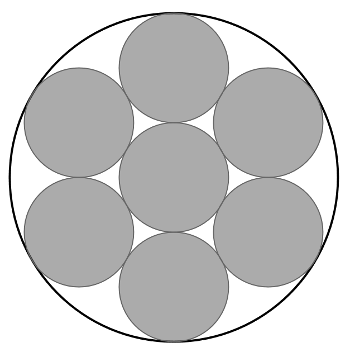
Quant mesura l'àrea blanca de la figura?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 10
4 punts
3 min
4 punts
•
3 min
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 11
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Tenim un tauler de $8\times8$ amb totes les caselles blanques, i una eina que ens permet canviar el color (de blanc a negre i de negre a blanc) de dues caselles contigües qualsevol. Per exemple:
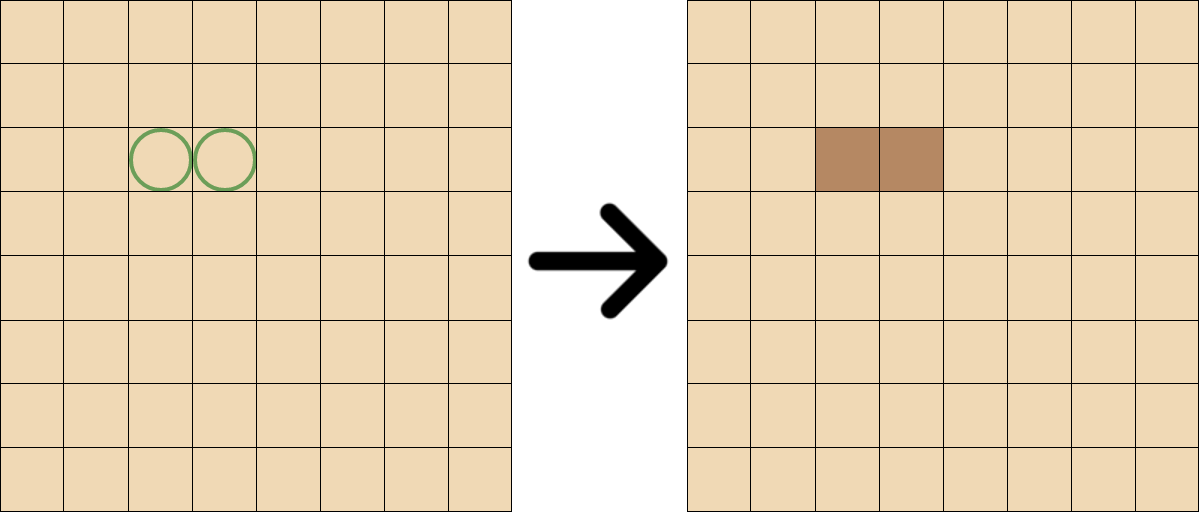
Quantes vegades hem d'usar l'eina per convertir el tauler en un tauler d'escacs?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 12
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Quin percentatge dels números entre l'$1$ i el $10\,000$ (ambdós inclosos) són capicua?
Alguns exemples de números capicua són: $4,\; 454,\; 22,\; 1331$.
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 13
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Volem situar a una fila del tauler d'escacs un rei i dues torres amb les següents condicions:
- El rei està a una de les dues caselles centrals:

- Una torre està a l'esquerra del rei i l'altra a la dreta. Per exemple:

De quantes formes diferents podem col·locar les tres peces, complint les condicions anteriors?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 14
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Conta la llegenda, que el rei hindú Sheram, entusiasmat pel joc dels escacs que havia inventat el seu súbdit Seta, va decidir recompensar-lo concedint-li allò que demanés.
Seta va demanar el següent: per cadascuna de les 64 caselles del tauler d'escacs, rebria una certa quantitat d'arròs: cada dia el doble que el dia anterior.
Així, el primer dia va rebre $1$ gra d'arròs, el segon dia $2$ grans, el tercer dia $4$ grans, etc.
En total, quina quantitat li hauria de donar Sheram al seu súbdit per complir la promesa?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 15
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Dos amics juguen a un joc amb les següents normes:
- Inicialment situen una torre a la cantonada de baix a l'esquerra d'un tauler d'escacs.
- En torns alternatius, cadascun d'ells mou la torre tantes caselles com vol, però només cap a dalt o cap a la dreta.
- Qui mou la torre a la casella de dalt de tot a la dreta, guanya la partida.
Aquest és un exemple de partida, en què el segon jugador (vermell) guanya:
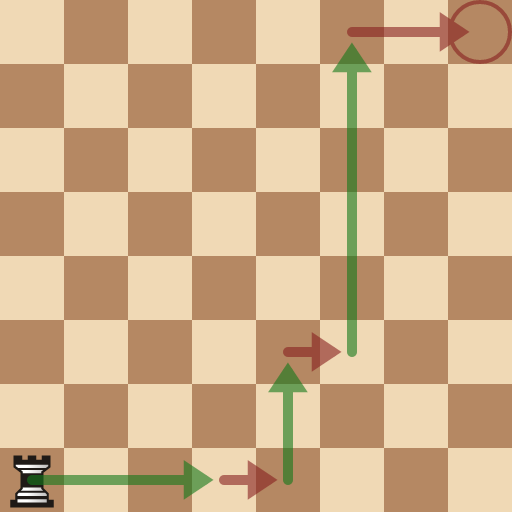
Si tots dos juguen tan bé com poden, intentant guanyar o perdre el més tard possible, quants cops es mourà la torre?
Degut a que la solució no està entre les opcions disponibles, aquest problema ha quedat anul·lat.
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Concurs 2n d'ESO
Estudiants que cursen 2n d'ESO o un curs inferior.
| # | Posició | Usuari | Punts | Respostes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Gauss | Gauss | 80,75 | ◌ | |||||||||||
| 2. | Jofre_T... | Jofre_Torras | 74,25 | ◌ ◌ | |||||||||||
| 3. | Arnausoler | Arnausoler | 53,25 | ◌ ◌ ◌ | |||||||||||
| 4. | ireneruiz | ireneruiz | 50,5 | ◌ | |||||||||||
| 5. | Adriana... | Adrianandreu3 | 39,75 | ◌ | |||||||||||
| 6. | aruiz2003E | aruiz2003E | 30,75 | ◌ | |||||||||||
| 7. | Mariona | Mariona | 30,5 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ |
Concurs obert
Usuaris que han superat 2n d'ESO, professors, etc.
| # | Posició | Usuari | Punts | Respostes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | martiju... | martijuanola | 77,0 | ◌ ◌ | ||||||||||
| 2. | arnaupa... | arnaupadres | 76,0 | ◌ | ||||||||||
| 3. | lauraco... | lauraconejero11 | 66,75 | ◌ ◌ | ||||||||||
| 4. | Ssr | Ssr | 64,75 | ◌ ◌ ◌ ◌ | ||||||||||
| 5. | 469 | 469 | 64,0 | ◌ ◌ ◌ | ||||||||||
| 6. | asantosn | asantosn | 59,5 | ◌ | ||||||||||
| 7. | JPG | JPG | 55,75 | ◌ | ||||||||||
| 8. | Diflon | Diflon | 53,75 | ◌ | ||||||||||
| 9. | mariona... | mariona_navarro14 | 47,75 | ◌ ◌ | ||||||||||
| 10. | nerea | nerea | 46,75 | ◌ | ||||||||||
| 10. | pauulaa8 | pauulaa8 | 46,75 | ◌ | ||||||||||
| 12. | Cristina | Cristina | 45,5 | ◌ ◌ ◌ | ||||||||||
| 13. | PACOVES | PACOVES | 44,75 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||
| 14. | Jarolin | Jarolin | 42,5 | ◌ ◌ | ||||||||||
| 15. | Luis | Luis | 41,75 | ◌ | ||||||||||
| 16. | Tumi_1501 | Tumi_1501 | 39,75 | ◌ | ||||||||||
| 17. | carlosdo | carlosdo | 35,0 | ◌ ◌ ◌ | ||||||||||
| 18. | Paula | Paula | 33,25 | ◌ | ||||||||||
| 19. | S.g.g | S.g.g | 25,75 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||
| 20. | marcmon | marcmon | 22,0 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ |
Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.
| # | Posició | Usuari | Punts | Respostes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | TomeuAn... | TomeuAndreu | 92,75 | ||||||||||||||
| 2. | Diego12... | Diego123a73 | 92,0 | ◌ | |||||||||||||
| 3. | PolGarcia3 | PolGarcia3 | 90,75 | ||||||||||||||
| 4. | CesarMG | CesarMG | 87,0 | ◌ | |||||||||||||
| 5. | jreyes | jreyes | 83,25 | ||||||||||||||
| 6. | ErikF | ErikF | 82,75 | ||||||||||||||
| 7. | joanbr | joanbr | 80,75 | ◌ | |||||||||||||
| 8. | J.P.B | J.P.B | 80,5 | ◌ | |||||||||||||
| 9. | JoanAn | JoanAn | 79,75 | ||||||||||||||
| 10. | laiagc | laiagc | 77,25 | ◌ | |||||||||||||
| 11. | Thaïs | Thaïs | 74,75 | ◌ | |||||||||||||
| 12. | AlbaSol... | AlbaSolisGarcia | 73,5 | ◌ ◌ | |||||||||||||
| 13. | rubenvi... | rubenvinaros | 70,75 | ||||||||||||||
| 14. | polgm | polgm | 67,5 | ||||||||||||||
| 15. | AlvaroS... | AlvaroSalon | 63,0 | ◌ | |||||||||||||
| 16. | saruca | saruca | 59,75 | ◌ ◌ ◌ ◌ | |||||||||||||
| 17. | gmor | gmor | 58,5 | ||||||||||||||
| 18. | toniV | toniV | 57,5 | ||||||||||||||
| 19. | EloiOri... | EloiOrigami | 56,75 | ◌ ◌ ◌ ◌ | |||||||||||||
| 20. | ikerzr | ikerzr | 54,5 | ◌ | |||||||||||||
| 21. | ruben_42i | ruben_42i | 52,5 | ||||||||||||||
| 22. | anubis | anubis | 50,5 | ◌ | |||||||||||||
| 22. | narapeula | narapeula | 50,5 | ◌ | |||||||||||||
| 24. | uver | uver | 50,0 | ◌ | |||||||||||||
| 25. | megawar... | megawarret3000 | 40,5 | ||||||||||||||
| 26. | nadia.R.L | nadia.R.L | 38,75 | ◌ | |||||||||||||
| 27. | Guillem... | Guillem.C.M | 36,75 | ||||||||||||||
| 28. | FerranCBU | FerranCBU | 35,0 | ||||||||||||||
| 29. | @el_bic... | @el_bicho_cr7 | 34,5 | ||||||||||||||
| 29. | enriccat | enriccat | 34,5 | ◌ ◌ | |||||||||||||
| 31. | Pep123 | Pep123 | 33,0 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ | |||||||||||||
| 32. | lucia_t... | lucia_tedesco | 26,75 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ |
Llegenda
→ Resposta correcta
→ Resposta correcta més ràpida de la taula (+1 punt)
→ Resposta incorrecta



