Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.
Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.
La contrarellotge s'ha acabat amb èxit!
Enhorabona al guanyador de la prova oficial: 469!
Atenció: el problema 11 ha quedat anul·lat degut a un error en les opcions (cap opció contenia la resposta correcta).
Us esperem d'aquí dues setmanes amb la prova de 2n de batxillerat!
Problema 1
3 punts
1 min
30 s
3 punts
•
1 min
30 s
A quantes caselles diferents poc accedir un cavall d'escacs situat a una de les caselles centrals del tauler?

El cavall es pot moure a $8$ caselles diferents:

Problema 2
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Quants centímetres quadrats mesura l'àrea del següent retall d'un tauler d'escacs, si sabem que cada casella té $1\text{ cm}$ de costat?

A la figura trobem $4$ quadrats sencers enmig, i $8$ mitjos quadrats que podem juntar per formar $4$ quadrats més. Per exemple, els podem agrupar usant colors:

En total, els $8$ quadrats mesuren $8\text{ cm}^2$.
Problema 3
3 punts
1 min
30 s
3 punts
•
1 min
30 s
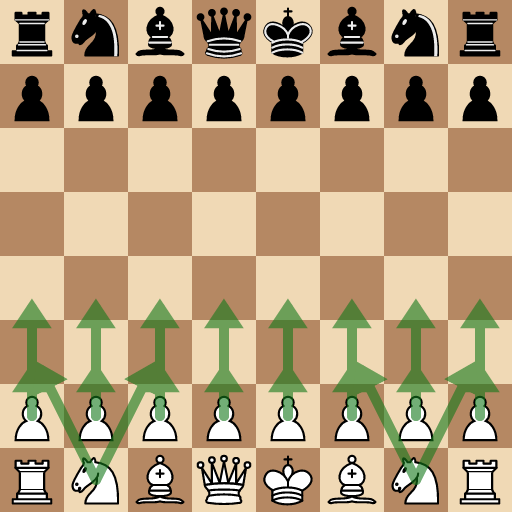
Quants moviments diferents pot fer el jugador d'escacs blanc per començar la partida? Recorda que inicialment, els peons es poden moure $1$ o $2$ caselles cap avant.
Inicialment es pot moure cada peó a una de dues caselles, $8\cdot2=16$ moviments diferents, o bé cadascun dels cavalls a una de dues posicions: $2\cdot2=4$. En total, hi ha $16+4=20$ moviments possibles:
Problema 4
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Quina és la diferència entre el número palíndrom més gran de $5$ xifres i el número palíndrom més petit de $4$ xifres?
Recordem que un número és un palíndrom si es llegeix igual d'esquerra a dreta que de dreta a esquerra. Per exemple, $123\,454\,321$ és un palíndrom.
Problema 5
3 punts
1 min
30 s
3 punts
•
1 min
30 s
En una cursa ciclista, sabem que Berta ha arribat immediatament després de Clara, i que Deva ha arribat entre Aina i Clara.
Qui ha arribat la primera?
Problema 6
4 punts
3 min
4 punts
•
3 min
Quants salts de cavall calen —com a mínim— per anar des de la casella de baix a l'esquerra fins a la casella de dalt a la dreta?

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 7
4 punts
3 min
4 punts
•
3 min
 Tenim $64$ boles d'igual aparença, i sabem que totes pesen el mateix, excepte una que pesa més que la resta. Usant una balança de dos pesos, quin és el mínim nombre de pesades que hem de fer per estar segurs d'identificar la bola més pesada?
Tenim $64$ boles d'igual aparença, i sabem que totes pesen el mateix, excepte una que pesa més que la resta. Usant una balança de dos pesos, quin és el mínim nombre de pesades que hem de fer per estar segurs d'identificar la bola més pesada?Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 8
4 punts
3 min
4 punts
•
3 min
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 9
4 punts
3 min
4 punts
•
3 min
Situem una torre, un cavall i un rei a la primera fila d'un tauler d'escacs de manera aleatòria. Quina és la probabilitat que el rei estiga enmig de les altres dues peces?

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 10
4 punts
3 min
4 punts
•
3 min
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 11
5 punts
4 min
30 s
5 punts
•
4 min
30 s
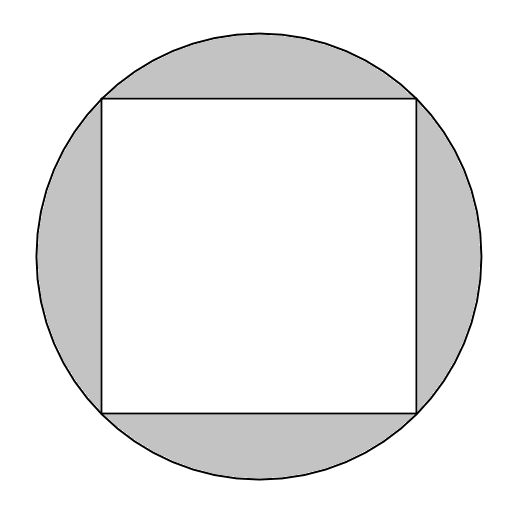
Aquest problema ha quedat anul·lat perquè la solució no es troba entre les opcions.
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 12
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 13
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 14
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Anomenem rei coix un rei d'escacs que només es pot moure cap a dalt o cap a la dreta:

Quants camins diferents pot recórrer un rei coix per anar de la cantonada de sota a l'esquerra del tauler d'escacs a la de dalt a la dreta?

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 15
5 punts
4 min
30 s
5 punts
•
4 min
30 s
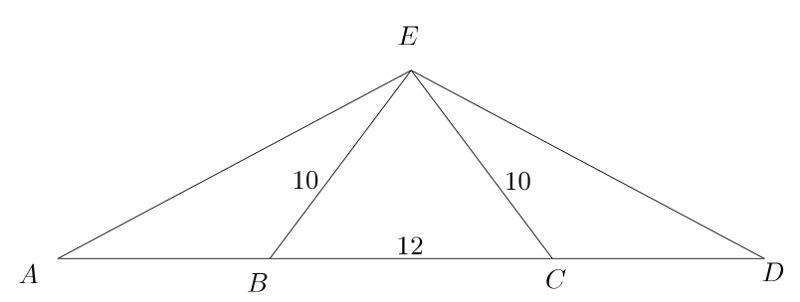
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Concurs 4t d'ESO
Estudiants que cursen 4t d'ESO o un curs inferior.
| # | Posició | Usuari | Punts | Respostes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | 469 | 469 | 72,5 | ◌ | ||||||||||||
| 2. | arnaupa... | arnaupadres | 67,0 | ◌ ◌ ◌ | ||||||||||||
| 3. | Arisb | Arisb | 60,5 | ◌ | ||||||||||||
| 4. | martiju... | martijuanola | 52,25 | ◌ ◌ ◌ | ||||||||||||
| 5. | Acma22 | Acma22 | 49,25 | ◌ | ||||||||||||
| 6. | angela_... | angela_clemente | 46,5 | ◌ ◌ | ||||||||||||
| 7. | albaem | albaem | 44,75 | ◌ | ||||||||||||
| 8. | FRANPASTOR | FRANPASTOR | 43,25 | ◌ | ||||||||||||
| 9. | Ssr | Ssr | 42,0 | ◌ ◌ ◌ | ||||||||||||
| 10. | Miquel | Miquel | 40,5 | ◌ ◌ ◌ | ||||||||||||
| 11. | lauraco... | lauraconejero11 | 38,25 | ◌ | ||||||||||||
| 12. | JPG | JPG | 37,5 | ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 13. | mariona... | mariona_navarro14 | 36,0 | ◌ | ||||||||||||
| 13. | MasterPlus | MasterPlus | 36,0 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 13. | Sarita34 | Sarita34 | 36,0 | ◌ ◌ | ||||||||||||
| 16. | Tumi_1501 | Tumi_1501 | 34,5 | ◌ | ||||||||||||
| 17. | carlosdo | carlosdo | 32,5 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 18. | andreagazu | andreagazu | 30,5 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 19. | andrea02 | andrea02 | 30,0 | ◌ | ||||||||||||
| 20. | miquelm | miquelm | 28,25 | ◌ | ||||||||||||
| 21. | Cristina | Cristina | 26,25 | ◌ ◌ ◌ ◌ | ||||||||||||
| 22. | Lorena | Lorena | 24,0 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 23. | pablopo... | pablopoker7 | 21,5 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ | ||||||||||||
| 24. | marcmon | marcmon | 20,5 | ◌ ◌ ◌ ◌ ◌ ◌ |
Concurs obert
Usuaris que han superat 4t d'ESO, professors, etc.
| # | Posició | Usuari | Punts | Respostes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|
| 1. | JMB | JMB | 63,0 | ◌ ◌ ◌ | |||
| 2. | PACOVES | PACOVES | 60,25 | ◌ ◌ | |||
| 3. | AndreuV... | AndreuVallcaneras | 59,0 | ◌ |
Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.
| # | Posició | Usuari | Punts | Respostes | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. | Andrea.... | Andrea.Sanchez | 78,25 | ||||||||||||
| 2. | Oliver.XA | Oliver.XA | 77,75 | ◌ | |||||||||||
| 3. | JoanFP | JoanFP | 61,25 | ◌ | |||||||||||
| 4. | Frances... | Francesc162005 | 54,25 | ◌ ◌ ◌ ◌ ◌ | |||||||||||
| 5. | Flac2 | Flac2 | 45,0 | ◌ ◌ | |||||||||||
| 6. | gmor | gmor | 44,75 | ||||||||||||
| 7. | enriccat | enriccat | 31,75 | ◌ | |||||||||||
| 8. | rvivob | rvivob | 31,0 | ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ ◌ |
Llegenda
→ Resposta correcta
→ Resposta correcta més ràpida de la taula (+1 punt)
→ Resposta incorrecta



