Contrarellotge entrenament Cangur (2n de Batxillerat)
Diumenge, 4 de març de 2018 a les 19:00

Aquesta Contrarellotge consisteix en un recull de 15 problemes d'edicions passades de les Proves Cangur.

Els enunciats del Cangur són propietat de la Societat Catalana de Matemàtiques i Le Kangourou sans Frontières.

Premi: Taller al Museu de Matemàtiques de Catalunya


El primer classificat a la Contrarellotge guanyarà un val per 4 persones per visitar el Museu de Matemàtiques de Catalunya i realitzar el taller de «Les cúpules de Leonardo».

Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.

Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Problema 1
3 punts   •   1 min 30 s

He pesat la meua bicicleta. Quin dels pesos següents puc haver trobat?
A. $12\text{ kg}$
B. $0,\!5\text{ kg}$
C. $800\text{ g}$
D. $80\text{ kg}$
E. $800\text{ kg}$
En blanc
Mostra solució

Aquest problema és el problema 6 del Cangur de 1r nivell de 2007.

L'únic pes raonable és $12\text{ kg}$. Com a curiositat, l'Unió Ciclista Internacional estipula que el pes mínim d'una bicicleta de competició ha de ser $6,\!8\text{ kg}$.

Els pesos de $0,\!5\text{ kg}$ o $800\text{ g}$, ambdós menors d'un quilogram, són massa petits: són comparables a una ampolla d'aigua o un paquet d'arròs.

En canvi, un pes de $80\text{ kg}$ podria ser similar al d'una persona, i $800\text{ kg}$ és el que pesen alguns cotxes.

Problema 2
3 punts   •   1 min 30 s

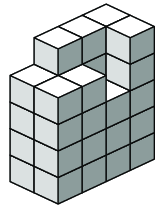
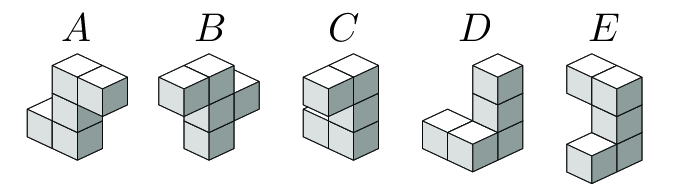
Quina de les peces següents necessitem per a completar el paral·lelepípede de la figura dreta?

A. La $A$.
B. La $B$.
C. La $C$.
D. La $D$.
E. La $E$.
En blanc
Mostra solució

Aquest problema és el problema 6 del Cangur de 1r nivell de 2011 a Catalunya.

L'única figura que encaixa és la $E$.

Problema 3
3 punts   •   1 min 30 s

Quin és el valor de $\frac12$ de $\frac23$ de $\frac34$ de $\frac45$ de $\frac56$ de $\frac67$ de $\frac78$ de $\frac89$ de $\frac9{10}$ de $1000$?
A. $250$
B. $200$
C. $150$
D. $100$
E. Un altre valor.
En blanc
Mostra solució

Aquest problema és el problema 5 del Cangur de 3r nivell de 2009.

Es tracta de calcular el valor de: $$1000\cdot\frac12\cdot\frac23\cdot\frac34\cdot\frac45\cdot\frac56\cdot\frac67\cdot\frac78\cdot\frac89\cdot\frac9{10}=\frac{1000}{10}=100$$ Tots els numeradors es cancel·len amb els denominadors, exceptuant el $10$ de l'última fracció, i per tant el resultat és $100$.

Problema 4
3 punts   •   1 min 30 s

Tenim sis punts marcats sobre una quadrícula:

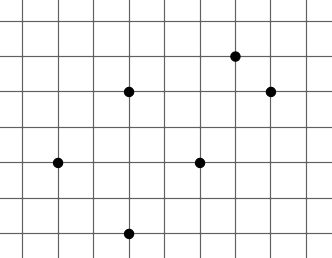
Quina de les figures geomètriques següents no pot tenir tots els vèrtexs en alguns d'aquests punts?

A. Un quadrat.
B. Un paral·lelogram que no sigui un rombe.
C. Un trapezi.
D. Un triangle obtusangle.
E. Totes les figures esmentades a A, B, C i D poden tenir tots els vèrtexs en aquests punts.
En blanc
Mostra solució

Aquest problema és el problema 7 del Cangur de 3r nivell de 2010.

Les quatre figures de les opcions es poden construir:

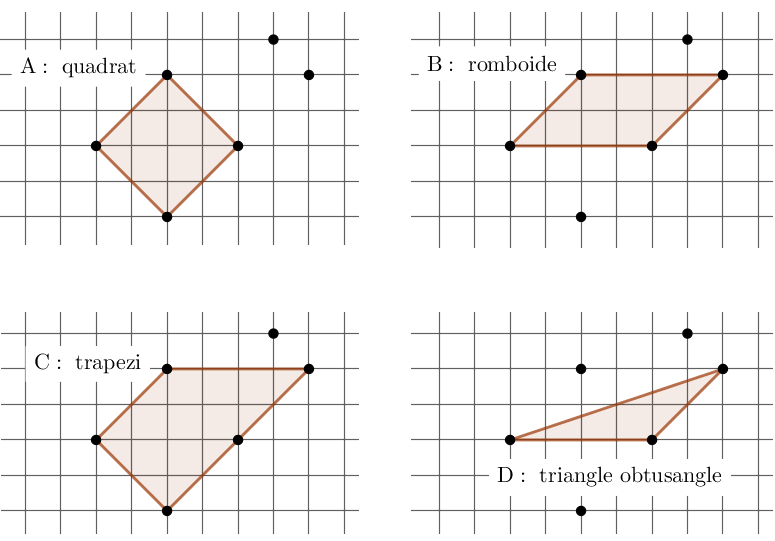
Problema 5
3 punts   •   1 min 30 s

La família Cangur va anar a collir bolets i en va trobar $180$. Se'n va menjar $20$ per sopar i la resta els congelà o els posà a assecar. Va posar a assecar $40$ bolets més que els que va congelar.

Quants en va assecar?

A. $60$
B. $80$
C. $160$
D. $120$
E. $100$
En blanc
Mostra solució

Aquest problema és el problema 4 del Cangur de 1r nivell de 2012 al País Valencià.

Dels $180$ bolets que van collir, els en van quedar $160$ per assecar o congelar. Anomenem $x$ el nombre que bolets que van assecar, per tant l'enunciat ens diu que: $$x+(x-40)=160\quad\Rightarrow\quad 2x=200\quad\Rightarrow\quad x=100$$ Per tant, van assecar $100$ bolets.

Problema 6
4 punts   •   3 min

El meu carrer té $15$ cases. Jo visc en el número $12$, que és la darrera casa del costat dels números parells. El meu cosí viu a l'última casa de l'altre costat.

Quin número té la seva casa?

A. $5$
B. $7$
C. $9$
D. $13$
E. $17$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 7
4 punts   •   3 min

Durant un creuer pel Mediterrani s'organitzen quatre visites opcionals, i a cadascuna de les sortides hi va un $80\%$ dels passatgers. Quin és el percentatge més petit possible de passatgers que ha anat a totes les sortides?
A. $16\%$
B. $20\%$
C. $40\%$
D. $60\%$
E. $80\%$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 8
4 punts   •   3 min

Tenim els set nombres $-9,0,-5,5,-4,-1,-3$. N'agafem sis i els agrupem en parelles de manera que la suma dels elements de cada parella sigui la mateixa. Quin nombre no hem agafat?
A. $5$
B. $0$
C. $-3$
D. $-4$
E. $-5$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 9
4 punts   •   3 min

D'una certa funció $f$ en el conjunt dels nombres enters, se'n fa aquesta afirmació:

«Per a qualsevol $x$ parell, $f(x)$ és parell».

Si aquesta afirmació és falsa, quina de les proposicions següents podem assegurar que és certa?

A. Per a qualsevol nombre parell $x$, $f(x)$ és senar.
B. Per a qualsevol nombre senar $x$, $f(x)$ és parell.
C. Per a qualsevol nombre senar $x$, $f(x)$ és senar.
D. Hi ha un nombre parell $x$ que fa que $f(x)$ sigui senar.
E. Hi ha un nombre senar $x$ que fa que $f(x)$ sigui senar.
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 10
4 punts   •   3 min

La darrera xifra diferent de zero del nombre $K=2^{59}\cdot3^4\cdot5^{53}$ és:
A. $1$
B. $2$
C. $4$
D. $6$
E. $9$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 11
5 punts   •   4 min 30 s

La gràfica d'una funció $y=(a-x)(b-x)^2$, en què $a\lt b$, és una d'aquestes. Quina?

A. $A$
B. $B$
C. $C$
D. $D$
E. $E$
En blanc
Mostra solució

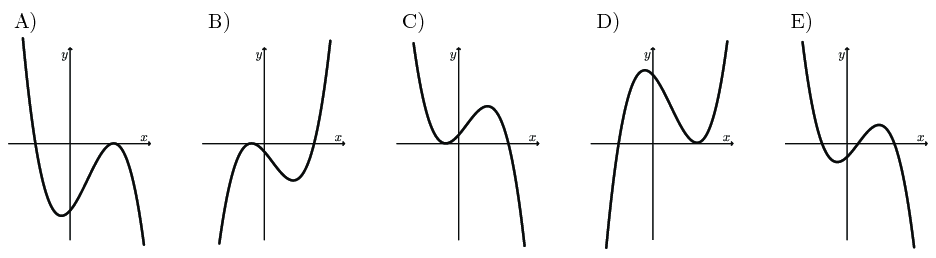
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 12
5 punts   •   4 min 30 s

Una caixa conté $900$ targetes numerades de $100$ a $999$, totes amb els nombres diferents. En Robert treu, de cop, unes quantes targetes i fa la suma de les xifres de cadascuna.

Quantes targetes ha de treure, com a mínim, per estar segur que tindrà tres targetes amb la mateixa suma de xifres?

A. $51$
B. $52$
C. $53$
D. $54$
E. $55$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 13
5 punts   •   4 min 30 s

El primer element d'una successió és $a_1=0$, i la resta compleixen: $$a_{n+1}=a_n+(-1)^nn$$ Si $a_k=2006$, quin és el valor de $k$?
A. $2006$
B. $2007$
C. $4013$
D. $4014$
E. Un altre
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 14
5 punts   •   4 min 30 s

Quants triangles hi ha amb perímetre igual a $20$ i amb els costats de longitud entera?
A. $6$
B. $7$
C. $8$
D. $10$
E. $12$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 15
5 punts   •   4 min 30 s

El quadrat de la figura té costat de longitud $1$. Llavors, el radi del cercle menut és:
A. $\sqrt2-1$
B. $\frac14$
C. $\frac{\sqrt2}4$
D. $1-\frac{\sqrt2}2$
E. $\left(1-\sqrt2\right)^2$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Concurs 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat o un curs inferior.

# Usuari Punts Respostes
1. 1r de Batxillerat  arnaupadres 85
◌
2. 4t d'ESO  JavierN 82
3. 4t d'ESO  PauCantos 79,25
◌
4. 4t d'ESO  Abel 75,75
◌
5. 1r de Batxillerat  martijuanola 72,75
◌ ◌
6. 2n de Batxillerat  Tungs 69,25
◌
◌ ◌
7. 4t d'ESO  VISI 68,5
◌
8. 2n de Batxillerat  Antoni 68,25
9. 3r d'ESO  Joana 67,75
◌ ◌
10. 2n de Batxillerat  MartiA_moià 59,25
◌ ◌
11. 2n de Batxillerat  AVM_Moià 58
12. 2n de Batxillerat  Gauss 57,5
◌
◌ ◌ ◌
13. 2n de Batxillerat  ÒscarP_Moià 56,5
◌
◌ ◌ ◌
14. 2n de Batxillerat  LSV_Moià 52,75
15. 2n de Batxillerat  isaaclemon 52,5
◌
◌
◌
16. 2n de Batxillerat  MFC_Moià 52
◌ ◌
17. 4t d'ESO  Diego123a73 46,75
◌
◌ ◌ ◌
18. 2n de Batxillerat  DesiBM_Moià 46,5
◌
◌ ◌
18. 2n de Batxillerat  fionasosamoianès 46,5
◌
◌
◌ ◌ ◌ ◌ ◌
20. 2n de Batxillerat  AFR_Moià 46
◌ ◌
21. 2n de Batxillerat  Albert_Súria 40,75
◌
22. 2n de Batxillerat  MGC_Moià 39,75
23. 2n de Batxillerat  PBG_Moià 37,5
◌ ◌ ◌ ◌
24. 2n de Batxillerat  AbelB 37
◌
25. 2n de Batxillerat  ACG_Moià 36
25. 2n de Batxillerat  Sali 36
◌
◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
27. 2n de Batxillerat  emmaaor 34,75
◌
◌
◌ ◌
28. 2n de Batxillerat  jtorres8_moià 33,5
29. 1r de Batxillerat  Tumi_1501 33
◌ ◌

Concurs obert
Usuaris que han superat 2n de Batxillerat, professors, etc.

# Usuari Punts Respostes
1. Universitat  oriol 79,5
2. Curs indeterminat  Feral 60,5
3. Curs indeterminat  luca.passolini2017 53,25
4. Universitat  GAC_Moià 29,25
◌
◌ ◌

Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.

# Usuari Punts Respostes
1. Universitat  joelpp 100
1. Universitat  PauMB 100
3. Universitat  jllobera 97
4. Universitat  ikerzr 95
◌
5. Universitat  Enrique 88
6. 2n de Batxillerat  osantacreu 84,75
7. Curs indeterminat  JordiMOIÀ 81
8. Universitat  Euler 79,75
◌
9. Universitat  GBADIA 78,5
10. Curs indeterminat  uvercraft240 76
◌ ◌
11. Universitat  @soloenparalelo 74,25
12. Curs indeterminat  Nour 71,75
◌ ◌ ◌
◌
13. Universitat  AlvaroSalon 67,25
14. Universitat  Jordi3456 65,25
◌

Llegenda

  →   Resposta correcta

  →   Resposta correcta més ràpida de la taula (+1 punt)

  →   Resposta incorrecta