Contrarellotge entrenament Cangur (2n d'ESO)
Diumenge, 18 de febrer de 2018 a les 19:00

Aquesta Contrarellotge consisteix en un recull de 15 problemes d'edicions passades de les Proves Cangur.

Els enunciats del Cangur són propietat de la Societat Catalana de Matemàtiques i Le Kangourou sans Frontières.

Premi: Taller al Museu de Matemàtiques de Catalunya


El primer classificat a la Contrarellotge guanyarà un val per 4 persones per visitar el Museu de Matemàtiques de Catalunya i realitzar el taller de «Les cúpules de Leonardo».

Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.

Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Problema 1
3 punts   •   1 min 30 s

Quants enters hi ha entre $2,018$ i $19,36$?
A. $14$
B. $17$
C. $15$
D. $16$
E. Més de $17$
En blanc
Mostra solució

Aquest problema està basat en el problema 3 del Cangur de 1r nivell de 2009.

Hi ha $19-2=17$ enters, que són: $$3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19$$

Problema 2
3 punts   •   1 min 30 s

Quina de les peces següents:

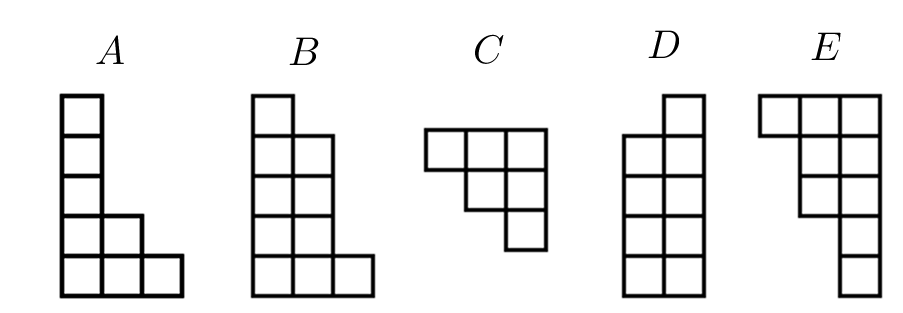
Encaixa amb aquesta peça:

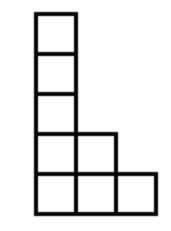
Per formar un rectangle?

A. La $A$.
B. La $B$.
C. La $C$.
D. La $D$.
E. La $E$.
En blanc
Mostra solució

Aquest problema està basat en el problema 2 del Cangur de 1r nivell de 2007.

Amb la peça de l'opció $B$ podem obtindre un rectangle:

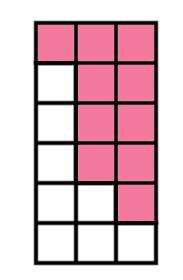
Problema 3
3 punts   •   1 min 30 s

Un cotxe ha recorregut $36$ km en $40$ minuts. A quina velocitat mitjana ha anat?
A. $18\text{ km/h}$
B. $36\text{ km/h}$
C. $38\text{ km/h}$
D. $54\text{ km/h}$
E. $72\text{ km/h}$
En blanc
Mostra solució

Aquest problema està basat en el problema 2 del Cangur de 1r nivell de 2011.

Calculem la velocitat d'aquest cotxe en quilòmetres per hora amb factors de conversió: $$v=\frac{36\text{ km}}{40\text{ min}}\times\frac{60\text{ min}}{1\text{ h}}=54\text{ km/h}$$ També ho hauríem pogut calcular amb una regla de tres.

Problema 4
3 punts   •   1 min 30 s

Quin és el mínim nombre de xifres que hem d'esborrar al nombre $12323315$ per tal de formar un nombre capicua?
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
En blanc
Mostra solució

Aquest problema està basat en el problema 4 del Cangur de 1r nivell de 2009.

En primer lloc, és evident que hem de traure el $5$ del final, ja que només tenim un $5$: $$1232331$$ Ara, que ja tenim dos $1$s als extrems, podem provar a esborrar cadascuna de les cinc xifres centrals: $$132331, 122331, 123331, 123231, 123231$$ Però en cap cas hem obtingut un nombre capicua. Esborrant una xifra més, sí que podem aconseguir-ho (esborrant l'últim $3$ del primer dels nombres de la llista anterior): $$13231$$ Per tant, hem hagut d'esborrar $3$ xifres com a mínim.

Problema 5
3 punts   •   1 min 30 s

Quants nombres de quatre xifres podem escriure amb la condició que cada xifra (excepte, lògicament, l'última), sigui dues unitats més gran que la que té immediatament a la dreta?
A. $4$
B. $5$
C. $6$
D. $7$
E. $8$
En blanc
Mostra solució

Aquest problema està basat en el problema 5 del Cangur de 1r nivell de 2008.

Començant per la xifra de les unitats, anirem completant tot el nombre: $$0 \rightarrow 20 \rightarrow 420 \rightarrow 6420$$ $$1 \rightarrow 31 \rightarrow 531 \rightarrow 7531$$ $$2 \rightarrow 42 \rightarrow 642 \rightarrow 8642$$ $$3 \rightarrow 53 \rightarrow 753 \rightarrow 9753$$ Si la xifra de les unitats és $4$, la xifra dels milers hauria de ser $10$, i això no pot ser. Per tant, hi ha $4$ nombres de quatre xifres amb aquesta propietat.

Problema 6
4 punts   •   3 min

A la següent graella $2\times2$ posem els nombres $2,3,4$ i un altre nombre que no sabem quin és.

La suma dels nombres de la primera fila dóna $9$, i la suma dels nombres de la segona fila dóna $6$.

Quin és el nombre que desconeixem?

A. $5$
B. $6$
C. $7$
D. $8$
E. $4$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 7
4 punts   •   3 min

Quants nombres naturals de $3$ xifres compleixen que el producte de les seues xifres és igual a $9$?
A. $2$
B. $3$
C. $4$
D. $5$
E. $6$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 8
4 punts   •   3 min

Dividim un cub d'un metre d'aresta en cubs d'un decímetre cúbic de volum.

Si col·loquem els cubs petits un damunt de l'altre, quina altura assoliran?

A. $100\text{ m}$
B. $1\text{ km}$
C. $10\text{ km}$
D. $1000\text{ km}$
E. $10\text{ m}$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 9
4 punts   •   3 min

Dividim una tira de paper en nou triangles equilàters com es veu a la figura. Quin polígon podem obtenir si dobleguem la tira per les línies de punts?

A. Un triangle
B. Un quadrilàter
C. Un hexàgon
D. Un octàgon
E. Un polígon de nou costats
En blanc
Mostra solució

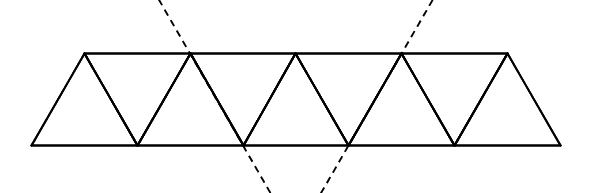
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 10
4 punts   •   3 min

Pintem tots els nombres naturals amb els colors roig, blau, groc o verd de la següent manera: $$ \begin{array}{c} 1: \text{roig}\\ 2: \text{blau}\\ 3: \text{groc}\\ 4: \text{verd}\\ 5:\text{roig}\\ 6: \text{blau}\\ 7: \text{groc}\\ 8: \text{verd}\\ \cdots \end{array}$$ Si sumem un nombre roig i un nombre groc, de quin color serà el resultat?
A. De qualsevol color
B. Roig o verd
C. Groc o verd
D. Blau o verd
E. Verd
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 11
5 punts   •   4 min 30 s

Copiem un nombre de dues xifres a la dreta del mateix nombre, obtenint un nombre de quatre xifres. Quantes vegades és més gran el nombre de quatre xifres que el de dues xifres?
A. $100$
B. $10$
C. $1000$
D. $1001$
E. $101$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 12
5 punts   •   4 min 30 s

En Bernat ha pensat un nombre enter. L'Anna l'ha multiplicat per $5$ o per $6$. El Josep ha sumat $5$ o $6$ al resultat de l'Anna. La Maria ha restat $5$ o $6$ al resultat del Josep i ha obtingut $73$.

Quin nombre havia pensat en Bernat?

A. $10$
B. $11$
C. $12$
D. $14$
E. $15$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 13
5 punts   •   4 min 30 s

Volem moure una fitxa sobre el tauler $3\times3$ de la figura de manera que passe per cada casella exactament una vegada. La fitxa es pot moure horitzontalment o verticalment, però no en diagonal.

A quina casella podem començar el joc?

A. A qualsevol casella negra.
B. A qualsevol casella de la columna central.
C. A qualsevol casella blanca.
D. Només a la casella central.
E. A qualsevol casella.
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 14
5 punts   •   4 min 30 s

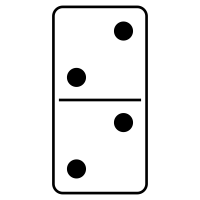Un joc del dòmino conté cada combinació possible de dos nombres entre el $0$ i el $6$, ambdós inclosos, incloent-hi dues vegades el mateix nombre. En total, es tracta de $28$ peces. Quants punts hi ha, en total, en les $28$ peces?
A. $84$
B. $105$
C. $126$
D. $147$
E. $168$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 15
5 punts   •   4 min 30 s

A la següent figura veiem com un cercle i un quadrilàter descomponen el pla en set regions:

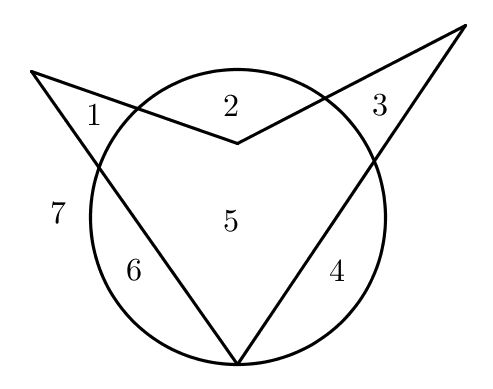
Quin és el nombre màxim de regions en què poden descompondre un pla un quadrilàter i un cercle?

A. $7$
B. $8$
C. $9$
D. $10$
E. $11$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Concurs 2n d'ESO
Estudiants que cursen 2n d'ESO o un curs inferior.

# Usuari Punts Respostes
1. 2n d'ESO  Alexl 83,75
2. 2n d'ESO  Sau 81,25
3. 2n d'ESO  Pauet37 80,75
4. 2n d'ESO  AlexNavarrov 77,25
5. 1r d'ESO  Pablo 77
6. 2n d'ESO  Aleix01 76,75
7. 1r d'ESO  GBH_Pius 76,25
◌
8. 2n d'ESO  M_E_S_M 72
9. 2n d'ESO  mmontull 71,75
10. 2n d'ESO  Jamer7 70,75
10. Primària  jaquerol 70,75
12. 1r d'ESO  ÒniaC_Moià 69,75
13. 1r d'ESO  CarlosBarrosoSellés 69,5
14. 1r d'ESO  bernard5 67,25
15. 2n d'ESO  visca 66,5
◌
16. 2n d'ESO  Leamsi_22 65
17. 2n d'ESO  MuFFiN 64,75
18. 1r d'ESO  polete 64,25
19. 2n d'ESO  MSR2n_Moià 63
20. 2n d'ESO  ASaSo_Moià 62,25
◌
20. 1r d'ESO  TheMark 62,25
22. 2n d'ESO  enocgirona2004 60,5
23. 2n d'ESO  albapertusa 57
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌
24. 1r d'ESO  andreu5 56
25. 2n d'ESO  DBR2B_Moià 54,5
26. 2n d'ESO  MCG2B_moià 53,75
◌
26. 2n d'ESO  noaporta22 53,75
◌
28. 2n d'ESO  paree16 51,75
29. 2n d'ESO  BDV2B_Moià 51,25
30. 2n d'ESO  LeireSoler 50
◌
31. 2n d'ESO  Gabisg04 49
◌ ◌ ◌
◌
32. 1r d'ESO  jana_i_nova 44,75
33. 2n d'ESO  LaiaMaso13 41,5
◌
34. 1r d'ESO  MartinaPB 40,75
35. 1r d'ESO  JHR_Moià 40,25
36. 2n d'ESO  sandra.pellicer 38,5
37. 2n d'ESO  RPL2BMoia 38
38. 2n d'ESO  marta.fabra 36
38. 2n d'ESO  Thaïs 36
40. 1r d'ESO  IGN_Moià 34,75
41. 2n d'ESO  EMC2nB_Moià 34,25
◌ ◌
42. 2n d'ESO  TJG3B_Moià 33,25
◌
◌
43. 2n d'ESO  LACS2nB_Moià 33
44. 1r d'ESO  ÀGN_Moià 32,75
◌
◌
45. 1r d'ESO  RGN_Moià 32,5
46. 2n d'ESO  REG2B_moia 25
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
47. 2n d'ESO  pintoj16@insmoianes.cat 24,75
48. 2n d'ESO  lenin 18,5
49. 2n d'ESO  nuriia_2eso 15,75
◌
50. 2n d'ESO  IFY2B_Moià 10

Concurs obert
Usuaris que han superat 2n d'ESO, professors, etc.

# Usuari Punts Respostes
1. 3r d'ESO  Joana 84,75
2. Curs indeterminat  Steffo 80
◌
◌
3. 4t d'ESO  JPG 77,75
4. 3r d'ESO  DJPIÑATA 75
◌
5. Universitat  Pau 67,75
◌
6. 4t d'ESO  Diego123a73 67,5
◌
7. 4t d'ESO  ruben_42i 64
◌
◌
8. Universitat  Alba 63,75
9. 4t d'ESO  masde 58,75
◌
◌
10. 3r d'ESO  Mireia 48
11. Professor/a  Mike 35
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
12. 1r de Batxillerat  marcmon 22
◌ ◌ ◌ ◌
◌ ◌ ◌ ◌
◌ ◌ ◌ ◌

Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.

# Usuari Punts Respostes
1. Curs indeterminat  @juliateixido 100
1. Universitat  FerranCBU 100
1. Curs indeterminat  ivanparedes 100
1. Universitat  maxep 100
1. Curs indeterminat  Racus555 100
1. Curs indeterminat  sfernandez 100
7. Universitat  ikerzr 99
7. Curs indeterminat  JoanAn 99
9. Universitat  Ana.11.17 90,75
10. Universitat  HugoMargalefSanchez 88
11. 4t d'ESO  crasclosa 85,5
12. Universitat  joanbr 83,75
13. Universitat  nadia.R.L 82,5
14. Universitat  Hamza 82,25
◌
15. 2n de Batxillerat  AlbaAlbó 80,75
16. Curs indeterminat  ErikF 79,25
◌
17. 4t d'ESO  Eva.v. 77,5
17. Universitat  polgm 77,5
19. Universitat  laiagc 77
20. Universitat  a 76
20. 3r d'ESO  Soletito 76
22. Universitat  arnaupadres 74
23. Universitat  anubis 73
24. Universitat  Imma 72,75
◌
25. 3r d'ESO  Dani.R 72
26. Universitat  saulbraza 71
◌
27. Universitat  Eugeni.C.S 69
28. Professor/a  cgimenez1986 68
◌
29. 2n d'ESO  Ale_Carol_FG 67,75
30. Universitat  HFOLIACOTS 66,75
31. Universitat  Euler 66
32. Universitat  narapeula 65
◌
33. Curs indeterminat  uvercraft240 63,5
34. Universitat  saruca 62,75
35. Universitat  juan7 62
36. Universitat  avrilvt 61
37. Universitat  SErgi0 60,5
38. Universitat  arnausanllehi 60
38. 6è de Primària  Pir2 60
◌
40. Curs indeterminat  zaibbuttsheraz 58,75
41. Curs indeterminat  marc555 57,5
42. 4t d'ESO  jiena 56
43. Universitat  Guillem.C.M 54,5
◌
44. Curs indeterminat  Mohamed 54,25
◌
45. 2n de Batxillerat  ericzer0 54
46. Universitat  martijuanola 52,5
47. Universitat  lucasmf 52
47. Curs indeterminat  Pulpo 52
49. 1r de Batxillerat  EloiOrigami 50
◌
◌
50. Universitat  jaumeam 49,75
51. Curs indeterminat  erolamena 49
52. 4t d'ESO  Jaume_ 44,25
53. Curs indeterminat  EricN 43,5
54. Universitat  Jose. 43
55. Curs indeterminat  RogerHT 36,75
56. Curs indeterminat  Pep 31,25
◌ ◌ ◌ ◌
◌
57. Universitat  aresrom 30,5
◌
58. Professor/a  Frederic 25
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌

Llegenda

  →   Resposta correcta

  →   Resposta correcta més ràpida de la taula (+1 punt)

  →   Resposta incorrecta