Contrarellotge entrenament Cangur (4t d'ESO)
Diumenge, 25 de febrer de 2018 a les 19:00

Aquesta Contrarellotge consisteix en un recull de 15 problemes d'edicions passades de les Proves Cangur.

Els enunciats del Cangur són propietat de la Societat Catalana de Matemàtiques i Le Kangourou sans Frontières.

Premi: Taller al Museu de Matemàtiques de Catalunya


El primer classificat a la Contrarellotge guanyarà un val per 4 persones per visitar el Museu de Matemàtiques de Catalunya i realitzar el taller de «Les cúpules de Leonardo».

Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.

Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Problema 1
3 punts   •   1 min 30 s

Elisa juga amb cubs i tetràedres. Quantes cares hi ha en total si té $6$ cubs i $4$ tetràedres?

A. $42$
B. $48$
C. $50$
D. $52$
E. $56$
En blanc
Mostra solució

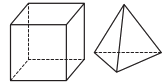
Aquest problema està basat en el problema 2 del Cangur de 2n nivell de 2011.

Cada cub té $6$ cares i cada tetràedre en té $4$. Per tant, en total tindrà: $$N_\text{cares} = 6\cdot6+4\cdot4=36+16=52$$

Problema 2
3 punts   •   1 min 30 s

Entre els nombres següents, quin és senar?
A. $20+18$
B. $2018$
C. $20^{18}$
D. $201-8$
E. $201\cdot8$
En blanc
Mostra solució

Aquest problema està basat en el problema 1 del Cangur de 2n nivell de 2009.

L'únic que és senar és: $$201-8=193$$

Problema 3
3 punts   •   1 min 30 s

La següent estrella està formada per $12$ triangles equilàters:

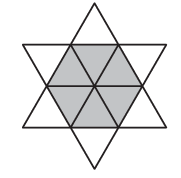
Té un perímetre de $36 \text{ cm}$. Quin és el perímetre de l'hexàgon gris?

A. $12\text{ cm}$
B. $6\text{ cm}$
C. $24\text{ cm}$
D. $30\text{ cm}$
E. $18\text{ cm}$
En blanc
Mostra solució

Aquest problema està basat en el problema 3 del Cangur de 2n nivell de 2009.

Fixem-nos que el perímetre de l'estrella està format per $2$ costats de cadascun dels triangles equilàters exteriors ($6$ en total).

Pel que fa a l'hexàgon, el perímetre ve donat per $1$ sol costat de cadascun dels triangles equilàters anteriors.

Per tant, el perímetre de l'hexàgon és la meitat que el de l'estrella: $$P_\text{hexàgon}=\frac{36\text{ cm}}2=18\text{ cm}$$

Problema 4
3 punts   •   1 min 30 s

Si tallem tots els vèrtexs d'un cub tal com es mostra al dibuix:

Quantes arestes té el poliedre que obtenim?

A. $26$
B. $30$
C. $36$
D. $40$
E. Una altra resposta.
En blanc
Mostra solució

Aquest problema està basat en el problema 6 del Cangur de 2n nivell de 2008.

Recordem que un cub té $6$ cares, $8$ vèrtexs i $12$ arestes.

El cos del dibuix té les $12$ arestes del cub, i a més ha afegit $3$ arestes a cada vèrtex. En total té: $$N_\text{arestes} = 12 + 3\cdot8=12+24=36$$

Problema 5
3 punts   •   1 min 30 s

Un rellotge és a sobre d'una taula de cara enlaire, i la busca dels minuts assenyala el nord-est.

Quants minuts han de passar fins que aquesta busca assenyali el nord-oest per primera vegada?

A. $45\text{ min}$
B. $40\text{ min}$
C. $30\text{ min}$
D. $20\text{ min}$
E. $15\text{ min}$
En blanc
Mostra solució

Aquest problema està basat en el problema 3 del Cangur de 2n nivell de 2012.

Com es veu a la següent Rosa dels vents:

Han de passar $45\text{ min}$ perquè la busca minutera assenyali el nord-oest.

Problema 6
4 punts   •   3 min

En Robert té nou monedes de $2$ cèntims. La seua cosina Berta té vuit monedes de $5$ cèntims.

Quin és el mínim nombre de monedes que s'han d'intercanviar per a tenir la mateixa quantitat de diners?

A. $4$
B. $5$
C. $8$
D. $12$
E. No es pot aconseguir.
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 7
4 punts   •   3 min

Una granota caça $12$ mosques en $3$ dies. Cada dia ha caçat més mosques que el dia anterior, i el tercer dia n'ha agafat menys que els dos primers dies junts.

Quantes mosques ha caçat la granota el tercer dia?

A. $4$
B. $5$
C. $6$
D. $7$
E. $8$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 8
4 punts   •   3 min

Un ascensor té capacitat per a $12$ adults o $20$ xiquets. Quants xiquets poden anar com a màxim amb $9$ adults?
A. $3$
B. $4$
C. $5$
D. $6$
E. $8$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 9
4 punts   •   3 min

Quin és el nombre mínim de punts que cal llevar de la figura següent, de manera que no queden $3$ punts alineats?

A. $1$
B. $2$
C. $3$
D. $4$
E. $7$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 10
4 punts   •   3 min

En tres partits de futbol, un equip ha marcat $3$ gols i n'ha encaixat $1$.

D'aquests partits, n'ha guanyat un, n'ha empatat un altre i ha perdut el tercer.

Quin és el resultat del partit que ha guanyat?

A. $3-0$
B. $2-0$
C. $1-0$
D. $2-1$
E. $0-1$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 11
5 punts   •   4 min 30 s

El nombre positiu $a$ és més petit que $1$, i el nombre $b$ és més gran que $1$.

Quin dels nombres següents és el més petit?

A. $\frac{a}{b}$
B. $b$
C. $a\times b$
D. $a+b$
E. La resposta depèn dels valor de $a$ i $b$.
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 12
5 punts   •   4 min 30 s

Una calculadora té espatllat el botó del dígit $1$. Per exemple, si teclegem $4121$, només mostra en pantalla el nombre $42$, sense espais.

L'Andreu ha teclejat un nombre de $6$ xifres en aquesta calculadora i a la pantalla ha aparegut $4009$.

Quants nombres diferents poden ser els que ha escriu l'Andreu?

A. $12$
B. $13$
C. $14$
D. $15$
E. $16$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 13
5 punts   •   4 min 30 s

Un noi sempre diu la veritat els dilluns i els dimarts, sempre menteix els dissabtes, i aleatòriament diu la veritat o menteix els altres dies de la setmana.

Durant set dies consecutius, li hem preguntat el seu nom, i durant els sis primers dies ens ha donat les respostes següents, en ordre: Pau, Jofre, Pau, Jofre, Pere, Jofre.

Què ha contestat el setè dia?

A. Pau.
B. Jofre.
C. Pere.
D. Carme.
E. Una altra resposta.
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 14
5 punts   •   4 min 30 s

Hem descompost un rectangle gran en tres rectangles petits. El primer fa $7\times11$ i el segon fa $4\times8$.

De totes les mesures possibles del tercer rectangle, quina és la que correspon a un rectangle amb l'àrea més gran possible?

A. $7\times8$
B. $3\times4$
C. $3\times8$
D. $1\times11$
E. $7\times11$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 15
5 punts   •   4 min 30 s

Les fraccions $\frac13$ i $\frac15$ estan situades a la recta numèrica:

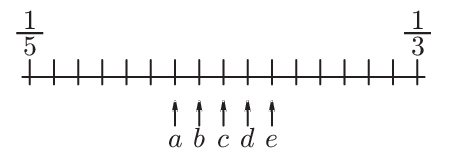
Quin punt correspon a la fracció $\frac14$?

A. $a$
B. $b$
C. $c$
D. $d$
E. $e$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Concurs 4t d'ESO
Estudiants que cursen 4t d'ESO o un curs inferior.

# Usuari Punts Respostes
1. 4t d'ESO  JavierN 94
2. 3r d'ESO  Joan_Vila 89
◌
3. 4t d'ESO  PauCantos 73
◌ ◌ ◌ ◌
4. 3r d'ESO  Bramio 71
5. 4t d'ESO  bet 69,25
◌
5. 4t d'ESO  npujolvent17 69,25
◌
◌
7. 3r d'ESO  Joana 67
◌ ◌ ◌ ◌ ◌
◌ ◌
8. 4t d'ESO  Diego123a73 65,75
◌ ◌ ◌
◌
9. 4t d'ESO  AGR_Moià 61,5
10. 4t d'ESO  JFB_Moià 60,5
11. 3r d'ESO  DJPIÑATA 58,5
◌
12. 4t d'ESO  JPG 57,75
◌ ◌ ◌ ◌ ◌
◌
13. 4t d'ESO  LaiaGarolera_Moià 51,5
14. 2n d'ESO  Gabisg04 51
◌
◌ ◌ ◌
15. 4t d'ESO  ETS_Moià 49,5
16. 4t d'ESO  GSV_Moià 47,75
◌ ◌
◌ ◌
◌
17. 4t d'ESO  FMG_MOIA 47,5
18. 3r d'ESO  HECTORGV 46
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌
19. 4t d'ESO  evine 43
20. 4t d'ESO  OriolTort_moia 42,5
◌
◌
21. 3r d'ESO  hgarciam 41,25
22. 4t d'ESO  MIHAELA 40,5
◌ ◌
23. 4t d'ESO  dlvc_moia 39,5
24. 4t d'ESO  Pololiveras 37
24. 4t d'ESO  Ssr 37
26. 4t d'ESO  doonald_12 35,25
◌
26. 4t d'ESO  gregoPV_Moià 35,25
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌
28. 3r d'ESO  afrancesl 34,25
◌ ◌ ◌ ◌ ◌
◌ ◌
◌
29. 3r d'ESO  Gmoraa 33
◌ ◌ ◌ ◌ ◌
◌
30. 4t d'ESO  GzkHM_Moià 32,25
◌
31. 4t d'ESO  DSM_Moia 31,75
◌ ◌ ◌ ◌
◌ ◌ ◌ ◌
32. 4t d'ESO  Lgm_Moià 31,25
◌ ◌
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
33. 4t d'ESO  e.aliberch_Moià 30
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌
34. 4t d'ESO  TTP_Moià 29,75
35. 4t d'ESO  EBC_Moià 28
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌
35. 4t d'ESO  JGC_Moià 28
◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
37. 4t d'ESO  MartaMoià 26,25
38. 4t d'ESO  S.g.g 24
◌ ◌ ◌ ◌
◌
◌ ◌ ◌
39. 4t d'ESO  Guillem_G_S_Moià 22
◌ ◌ ◌ ◌ ◌
◌

Concurs obert
Usuaris que han superat 4t d'ESO, professors, etc.

# Usuari Punts Respostes
1. Universitat  Antoni 91
2. Universitat  oriol 79
◌ ◌ ◌
◌
3. 1r de Batxillerat  Acma22 70,75
◌ ◌ ◌
4. 1r de Batxillerat  arnaupadres 67
◌ ◌ ◌ ◌ ◌
5. 1r de Batxillerat  martijuanola 66
◌ ◌ ◌ ◌
◌
6. Curs indeterminat  Feral 46,5
◌
◌
7. Curs indeterminat  mariona.moià 36
◌
8. Universitat  AVM_Moià 31,5
◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
9. 4t d'ESO  SDC_MOIA 29
◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌

Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.

# Usuari Punts Respostes
1. Curs indeterminat  Bresopau_07 100
1. Universitat  edward_elric 100
1. 3r d'ESO  TomeuAndreu 100
4. Universitat  MarquitosBrowning 98
5. Curs indeterminat  PedritoPC208 94,25
6. 2n de Batxillerat  AlbaAlbó 92,75
7. Professor/a  AlvarBorrell 90
8. Universitat  mohamedsarghini14 89,25
9. Universitat  Anthony.nai.nai.nai 79,5
10. Universitat  ANDREU 74,75
11. Universitat  berta.serra 71,25
12. Universitat  Superep 70
13. Universitat  ChumbaChumba 66,75
14. Universitat  Francesc162005 65
◌
15. Universitat  juan7 64,25
16. Universitat  kenneth 62,5
17. Universitat  iksaba 60
18. Universitat  Jordi3456 59
19. Universitat  saulbraza 57
20. Universitat  CARLES 55
21. Universitat  nlasus 53,5
◌
22. Curs indeterminat  mjoseN 52,75
◌ ◌ ◌
◌ ◌ ◌
23. Universitat  pepito_la_flor 46,5
◌ ◌ ◌
◌
24. Curs indeterminat  Dídac31 39
25. Universitat  joel 37,5
◌
26. Universitat  rvivob 25
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌

Llegenda

  →   Resposta correcta

  →   Resposta correcta més ràpida de la taula (+1 punt)

  →   Resposta incorrecta