Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.
Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.
Els problemes d'aquesta contrarellotge els han proposat l'Abel Doñate i l'Oriol Baeza, amb l'edició de Víctor López i les correccions de Cristian Reyes i Miquel Vilà.
Problema 1
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Un rellotge analògic marca les $\text{5:00}$. Quin angle formen les agulles?
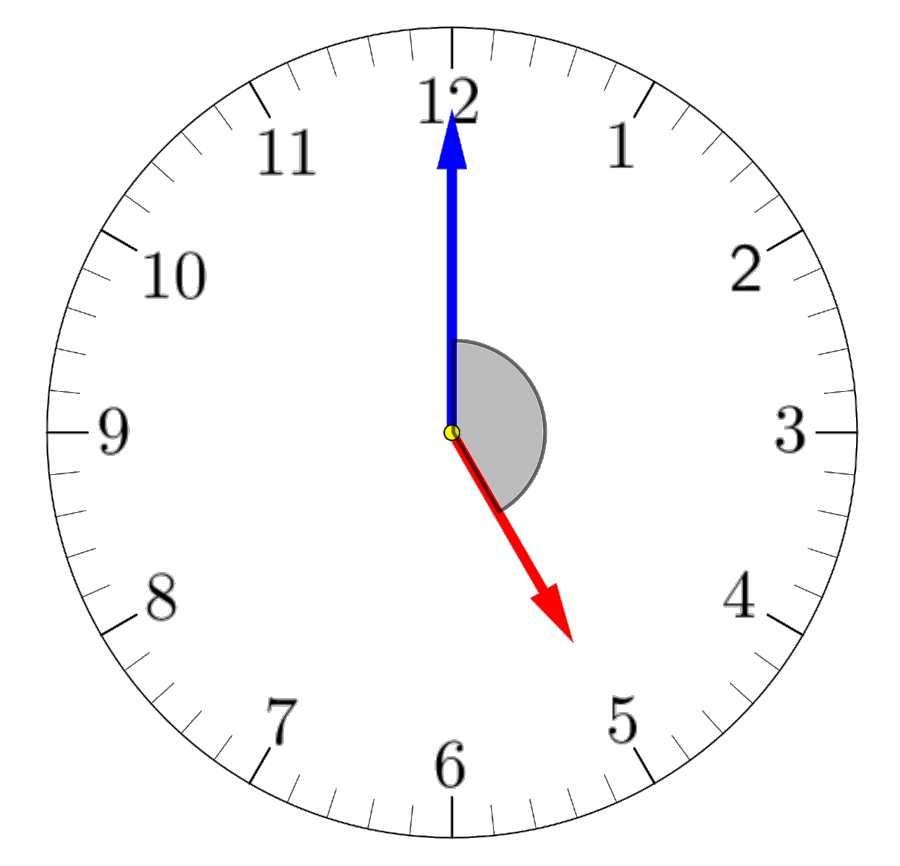
Si dividim els $360^\circ$ de la circumferència entre les $12$ hores, veiem que cada hora són $\frac{360}{12}=30^\circ$:
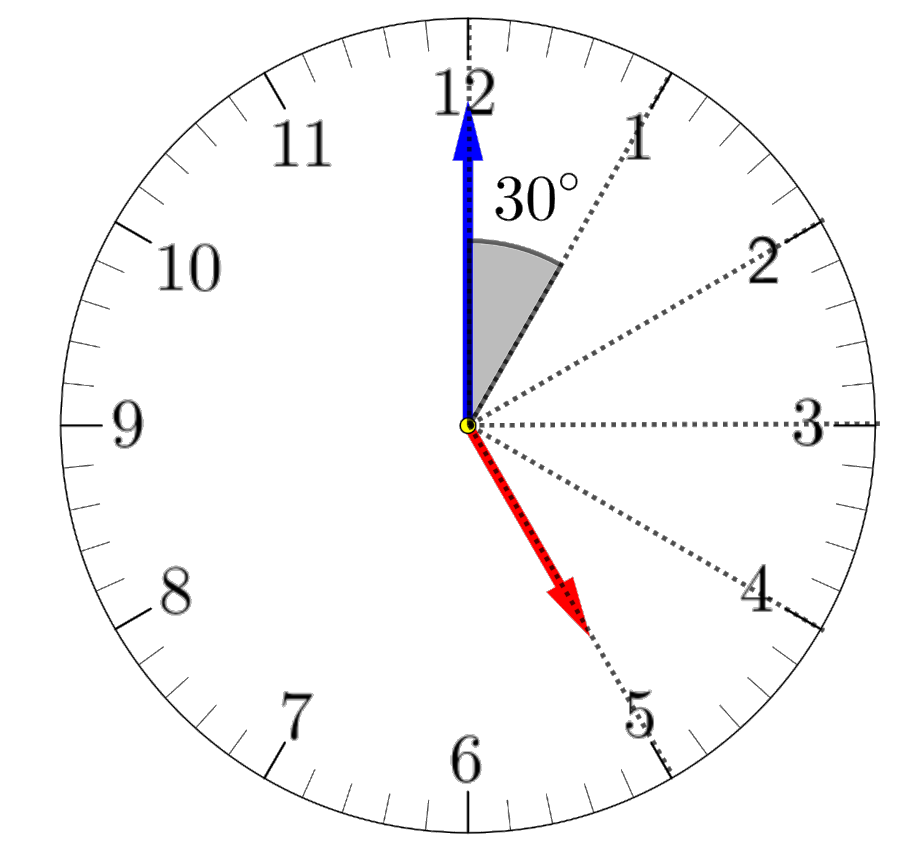
Per tant, $5$ hores són $5\times 30 = \boxed{150^\circ}$:
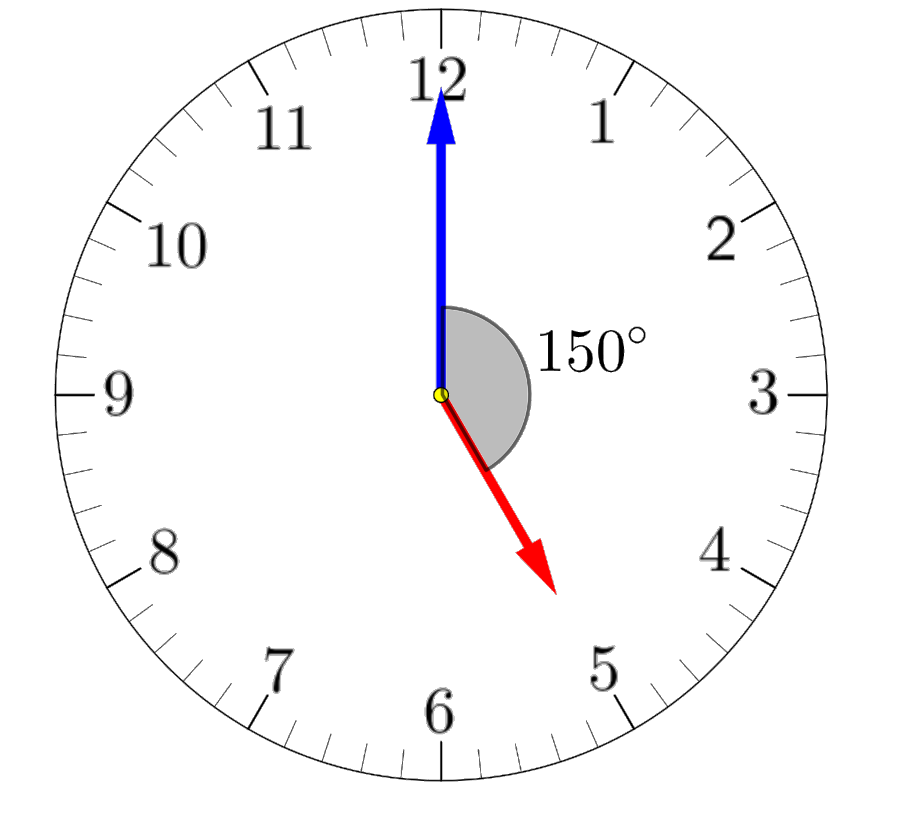
Problema 2
3 punts
1 min
30 s
3 punts
•
1 min
30 s
La diferència de dos nombres quadrats perfectes consecutius és $63$.
Quin és el quadrat gran?
Solució 1
L'enunciat ens planteja la següent equació: $$n^2 - (n-1)^2 = 63$$
Si expandim el quadrat de la resta $n-1$, obtenim: $$n^2-n^2+2n-1=63 \quad\implies\quad 2n-1=63 \quad\implies\quad n=32$$
Per tant, la solució és $32^2 = \boxed{1.024}$.
Solució 2
Podem estudiar el patró que segueix la diferència de dos quadrats perfectes consecutius: $$2^2-1^2=3$$ $$3^2-2^2=5$$ $$4^2-3^2=7$$ $$5^2-4^2=9$$ $$\cdots$$
I podem deduir que hi ha el següent patró: $$n^2-(n-1)^2=2n-1$$
Hem trobat la mateixa equació que en la primera solució: $2n-1=63$, de forma que $n=32$ i la solució és $32^2 = \boxed{1.024}$
Solució 3
Si ho enfoquem des d'un punt de vista geomètric, hem d'esbrinar què cal afegir a $(n-1)^2$ per transformar-lo en $n^2$:
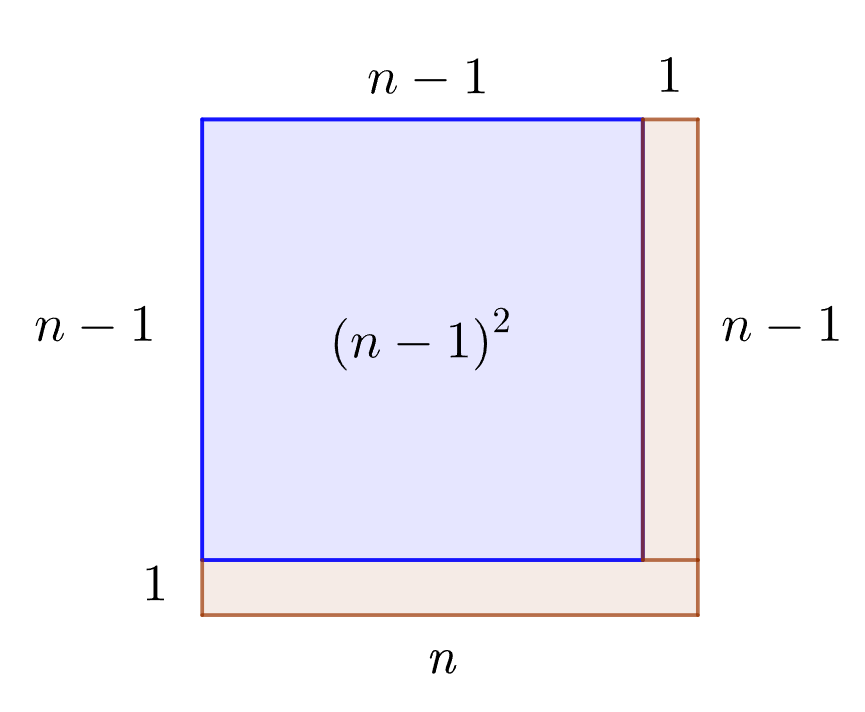
A la figura veiem que cal afegir $1\times n$ i $1\times(n-1)$, és a dir, $2n-1$, i aquesta és la diferència entre dos quadrats consecutius. És la mateixa equació que hem vist abans i resolent-la obtenim la mateixa solució.
Problema 3
3 punts
1 min
30 s
3 punts
•
1 min
30 s
De l'$1$ al $6$ tenim només el $3$. Observem que el comportament es repeteix cada $2\times 3 = 6$ números. Doncs, tenim $\boxed{10}$ enters: $$3,\, 9,\, 15,\, 21,\, 27,\, 33,\, 39,\, 45,\, 51,\, 57$$
Alternativament, els múltiples de $3$ fins a $60$ són $3\cdot1,\, 3\cdot2,\, 3\cdot3,\, 3\cdot4,\, \ldots,\, 3\cdot20$. Per tant, en tenim $20$. D'aquests, la meitat s'obtenen multiplicant $3$ per un nombre parell i, per tant, són múltiples de $2$. És a dir, ens en queden $\boxed{10}$.
Problema 4
3 punts
1 min
30 s
3 punts
•
1 min
30 s
La figura següent mostra una illa urbana d'habitatges de l'Eixample de Barcelona. A l'interior hi ha un jardí. Calcula la superfície habitada de l'illa (de color groc).
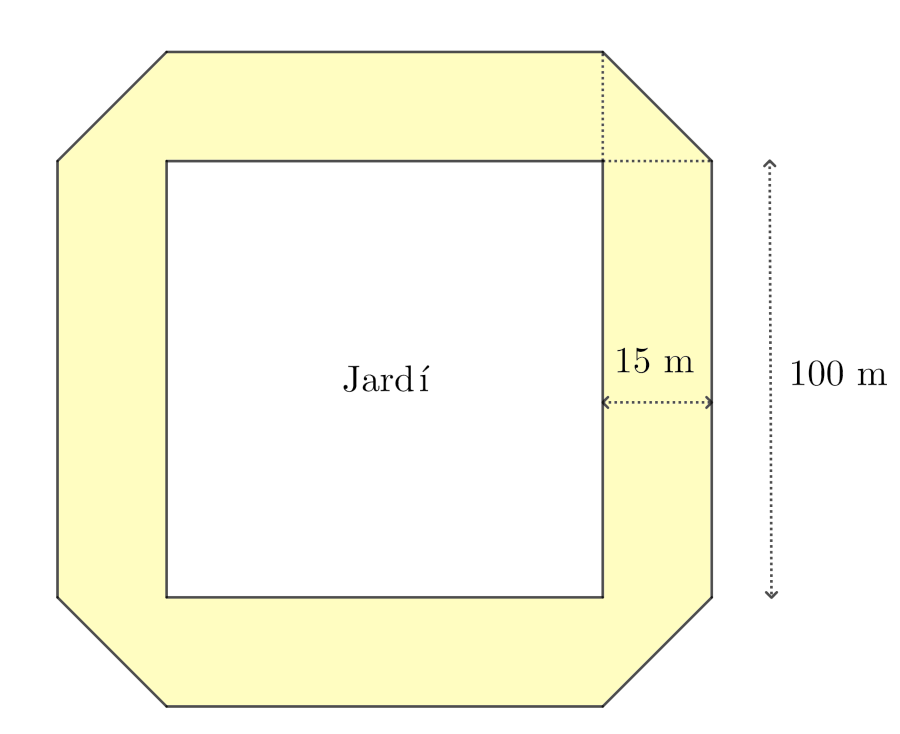
Podem dividir la part habitada de l'illa en $4$ triangles i $4$ rectangles iguals:
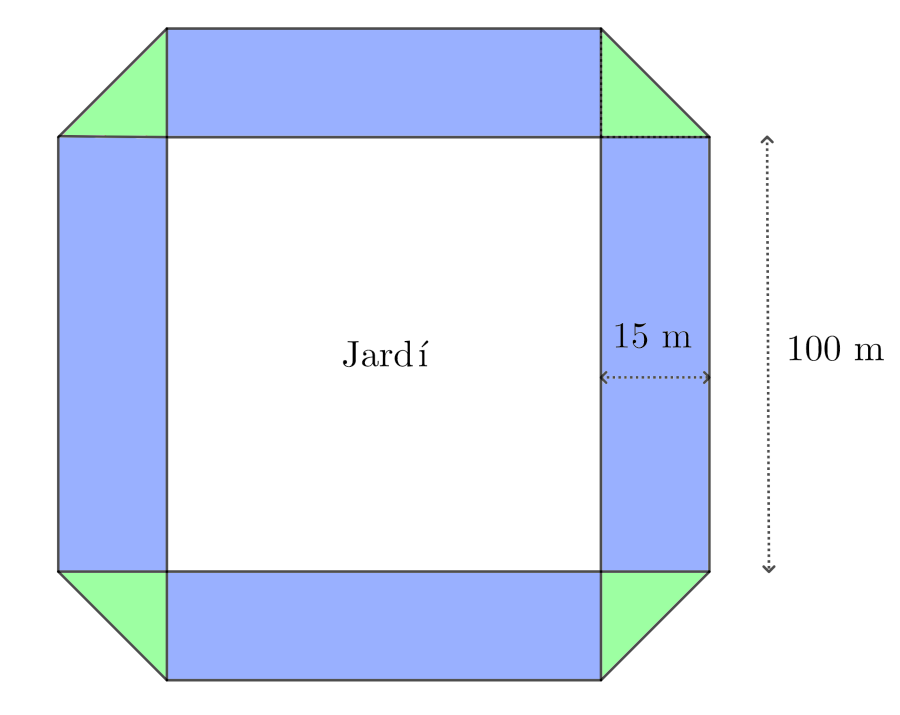
Que tenen les següents àrees: $$A_\text{rectangle} = 15\times100 = 1.500$$ $$A_\text{triangle} = \frac12 \times 15\times 15 = \frac{225}2$$
L'àrea habitada és: $$A_\text{habitada} = 4\times A_\text{rectangle} + 4\times A_\text{triangle} = 4\times 1.500 + 4\times \frac{225}2 = \boxed{6.450}$$
Problema 5
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Tenim tres ampolles iguals amb diferent quantitat d’aigua. Sabem que:
- La primera té $200\text{ ml}$.
- La segona té $\frac{5}{4}$ de la primera.
- La tercera té $\frac{2}{5}$ de la segona.
A més a més, sabem que si ajuntem l'aigua de les tres ampolles, l'ampolla queda mig plena.
Quina capacitat té cada ampolla?
Vegem la quantitat d'aigua que té cada ampolla:
- $200\text{ ml}$
- $\frac{5}{4}\times 200 = 250 \text{ ml}$
- $\frac{2}{5}\times250 = 100 \text{ ml}$
Entre les tres ampolles, tenen: $$200 + 250 + 100 = 550 \text{ ml}$$
Sabem que això és la meitat de la capacitat de l'ampolla, i per tant l'ampolla és de $2\times550=\boxed{1.100 \text{ ml}}$.
Problema 6
4 punts
3 min
4 punts
•
3 min
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 7
4 punts
3 min
4 punts
•
3 min
La Clara ha escrit un nombre format pels dígits dels $100$ primers nombres naturals positius seguits: $123456789101112\ldots$
Quina és la xifra número $150$ que hi apareix?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 8
4 punts
3 min
4 punts
•
3 min
La Carla fa $5$ dies que ha començat a llegir un llibre de $145$ pàgines. Com que l'ha trobat interessant, li ha dit al seu amic Roger que se'l llegeixi.
Al Roger, però, li agrada llegir els llibres al revés (primer l’última pàgina, després la penúltima, etc.). Això el fa anar a un ritme una mica lent: $3$ pàgines per dia. En canvi, la Carla llegeix a un ritme de $5$ pàgines per dia.
Quants dies portarà la Carla llegint quan es trobin?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 9
4 punts
3 min
4 punts
•
3 min
Una formiga camina per un cub d’aresta unitat, movent-se per les arestes. Comença i acaba el seu camí en un mateix vèrtex, i sense haver repetit cap aresta.
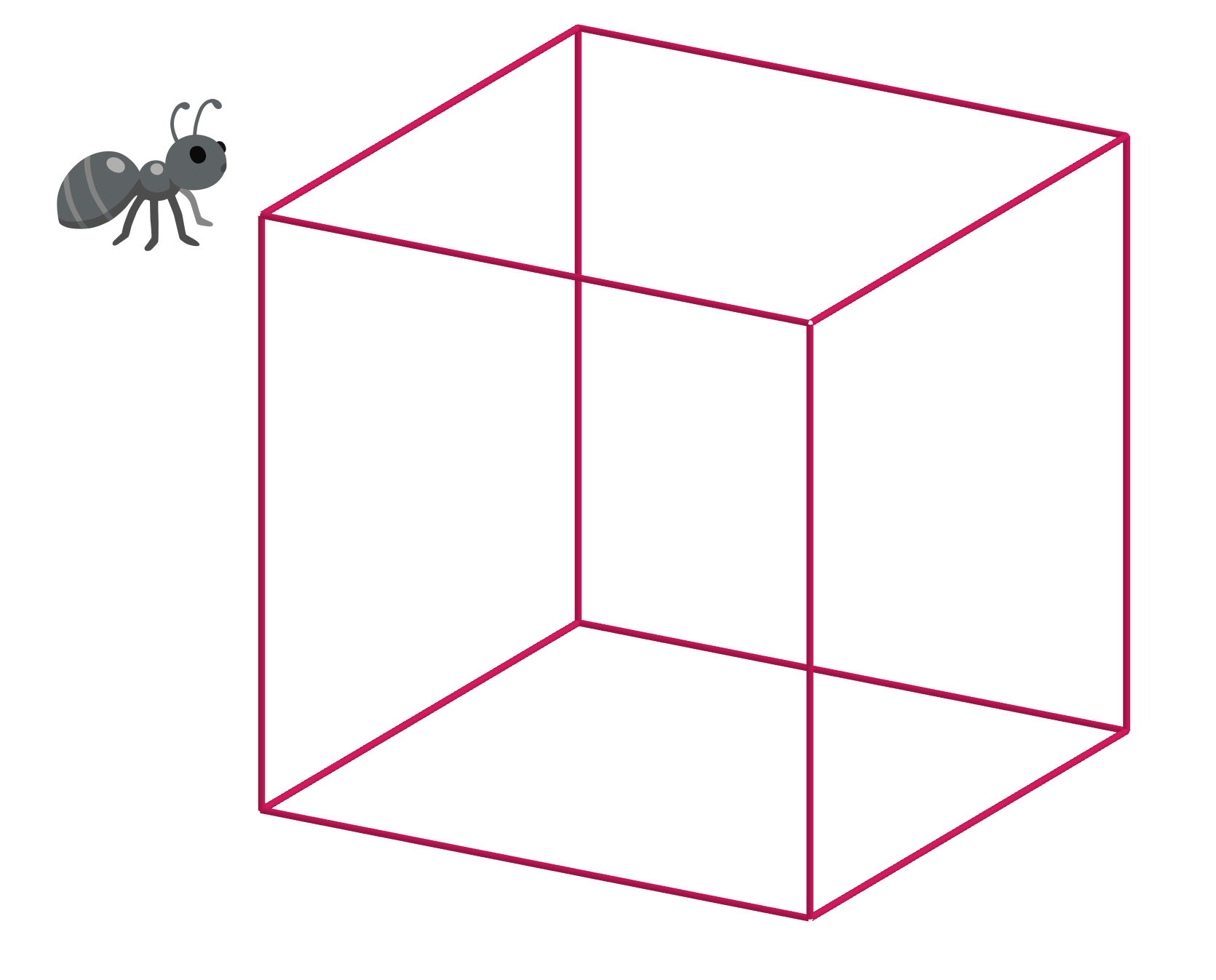
Quina d'aquestes opcions pot ser la longitud del camí?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 10
4 punts
3 min
4 punts
•
3 min
Si la roda blava gira a una velocitat de $40\text{ rpm}$ (revolucions per minut) i considerem els diàmetres de cada roda especificats al dibuix, quina velocitat i direcció té la roda vermella?
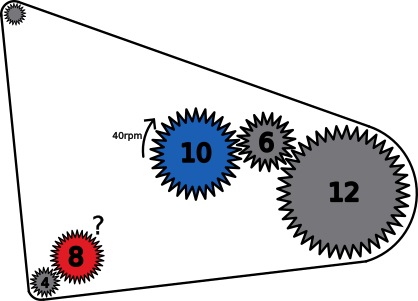
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 11
5 punts
4 min
30 s
5 punts
•
4 min
30 s
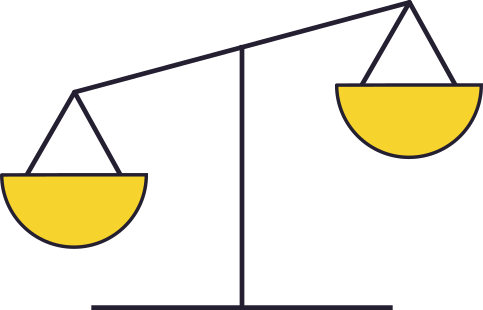
Tenim $27$ monedes tals que $26$ tenen exactament el mateix pes i una és lleugerament més pesada.
Si tenim una balança de plats com la de la figura, quin és el mínim nombre de pesades que ens assegura descobrir quina és la més pesada?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 12
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 13
5 punts
4 min
30 s
5 punts
•
4 min
30 s
De quantes maneres podem escriure $30$ com a suma de (mínim $2$) nombres naturals consecutius?
(Per exemple: $30 = 9 + 10 + 11$)
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 14
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Quants enters positius menors o iguals que $100$ tenen exactament tres divisors positius?
Per exemple, $6$ té quatre divisors: $1,2,3,6$, i no compleix la condició.
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 15
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Concurs 2n d'ESO
Estudiants que cursen 2n d'ESO o un curs inferior.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | Milena_Arsenyan | 85 |
◌
|
| 2. | Pacsfury | 84,25 |
|
| 3. | GuiuT | 80 |
◌
|
| 4. | Janito314 | 79 |
◌
◌
◌
|
| 5. | Júlia_manez | 76,25 |
◌
|
| 6. | Nil_Sarkar | 75,75 |
|
| 7. | Ferran.V | 75,25 |
|
| 8. | MarcelM | 74,75 |
|
| 9. | MarwaSemmane0 | 73 |
|
| 10. | AbrilPR | 71,75 |
◌
|
| 10. | Rodrigo26 | 71,75 |
◌
◌
◌
|
| 12. | TerryRaptor2000 | 69,25 |
◌
|
| 13. | AleixK | 67,75 |
|
| 14. | Luka_Shelegia | 67,25 |
|
| 15. | Truita_de_carbassó | 66,75 |
|
| 16. | Montserrat | 66,5 |
|
| 17. | spasalodos12@padredamiansscc.net | 65,25 |
◌
|
| 18. | Pol29 | 64,5 |
|
| 19. | Abrilparésbarbosa | 64,25 |
◌
|
| 20. | ADRlÀ12345 | 63,25 |
|
| 21. | BRO | 63 |
|
| 22. | Cr | 61,75 |
◌
◌
|
| 22. | RocketPit_12 | 61,75 |
◌
|
| 24. | DidacLinares | 61,5 |
|
| 25. | isaac | 61,25 |
|
| 26. | Chloe | 60,75 |
◌
◌
◌
|
| 27. | OnaCasals2205 | 60 |
◌
◌
◌
◌
|
| 28. | Arletii_1237 | 59,75 |
|
| 29. | 123ASDG | 59,25 |
◌
|
| 30. | Kalajary27 | 58,5 |
|
| 31. | Pausalva | 56,75 |
◌
◌
◌
|
| 32. | Asmaa-Laaraj-Zouba15 | 56,25 |
◌
|
| 32. | MartiGC | 56,25 |
◌
◌
|
| 34. | geometrika | 55,25 |
|
| 35. | Chimchu18 | 55 |
◌
|
| 35. | MarcML@Madina. | 55 |
◌
◌
◌
◌
|
| 37. | Ignasi2000 | 54,75 |
◌
◌
|
| 37. | sara@perez.2.0.1.2. | 54,75 |
◌
◌
|
| 39. | Marisol5@CR | 54,25 |
|
| 39. | Navajas | 54,25 |
◌
|
| 41. | Muncaster | 53,75 |
◌
◌
◌
|
| 41. | Tikus75 | 53,75 |
◌
◌
◌
|
| 43. | jaulora | 52,75 |
◌
|
| 44. | AmayaD | 52,5 |
|
| 44. | Lluc_12 | 52,5 |
|
| 46. | BielGT | 52,25 |
|
| 47. | ahanganu | 51,75 |
|
| 48. | JordiLlibre | 51,25 |
◌
|
| 49. | AS | 51 |
◌
|
| 49. | Iria_Moreno | 51 |
◌
◌
|
| 51. | ARNAU_RI | 50,5 |
◌
◌
|
| 51. | the_real_goat | 50,5 |
◌
|
| 53. | ThorB | 50,25 |
|
| 54. | Maia | 50 |
◌
|
| 55. | Eric07 | 49,75 |
|
| 56. | NoraJuliaMora | 48,75 |
◌
|
| 57. | AlejandroCM | 48,5 |
◌
|
| 58. | Mates_p77 | 48,25 |
◌
|
| 59. | Pir2 | 47,75 |
◌
|
| 60. | gabibvv | 47 |
|
| 60. | UnaiPérezFernández | 47 |
◌
◌
◌
◌
◌
◌
|
| 62. | marc.bertran | 46,75 |
|
| 63. | lalau27 | 45,5 |
◌
◌
◌
|
| 64. | ElCangur | 44,5 |
◌
◌
◌
|
| 65. | Plumier | 43,75 |
◌
◌
|
| 65. | victorito | 43,75 |
◌
|
| 67. | Alroma2709 | 43,5 |
|
| 67. | Aro@.20 | 43,5 |
|
| 67. | Guillem5 | 43,5 |
|
| 70. | PolSM | 43 |
◌
|
| 71. | Alexi@9 | 42,5 |
◌
◌
|
| 72. | GUGI | 42,25 |
◌
|
| 72. | RoboPau14 | 42,25 |
◌
◌
◌
|
| 74. | arnau2013 | 41,75 |
◌
◌
◌
◌
◌
◌
◌
|
| 75. | Ellen.Massanet | 40,5 |
◌
|
| 76. | LlucF | 40,25 |
|
| 77. | B777 | 39,75 |
◌
◌
◌
|
| 77. | Sofía-3I-ATLAS | 39,75 |
◌
◌
◌
◌
◌
◌
◌
|
| 79. | BlaiLT | 39 |
◌
|
| 80. | Origami2.0 | 33,25 |
|
| 81. | ElCaAn89 | 32,5 |
|
| 82. | Núria.Romero.Vilas | 32 |
◌
|
| 83. | ErikaMassanet@madina | 31 |
◌
|
| 84. | 25amirelhaouariaddali | 29,5 |
◌
|
| 84. | Bruna15 | 29,5 |
|
| 86. | naiam | 29,25 |
◌
◌
◌
|
| 87. | Irina | 28,75 |
|
| 88. | Vegaa | 28,25 |
|
| 89. | Milmanda | 28 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 90. | Elna | 27,75 |
◌
◌
◌
|
| 90. | Nico_Bonet | 27,75 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 92. | ValèriaSoléLafuerza | 27 |
◌
|
| 93. | tutusaus | 24,5 |
◌
|
| 94. | bbosch7@guissona.fedac.cat | 24,25 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
Concurs obert
Usuaris que han superat 2n d'ESO, professors, etc.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | arakelov | 90 |
|
| 2. | ncf92 | 89 |
|
| 3. | PauMartínezSánchez | 87 |
|
| 4. | Frogrammer | 85,25 |
|
| 5. | OG_JAP | 85 |
|
| 6. | rawalpi | 84 |
|
| 7. | lluc.galindo | 83,25 |
|
| 8. | eva.pascual | 81,25 |
|
| 8. | MCuadros | 81,25 |
◌
|
| 10. | Xpro02272 | 79 |
◌
◌
|
| 11. | OGNHGPKMN | 78,75 |
|
| 12. | Cristian_García | 78,25 |
|
| 13. | OGWHH | 77,75 |
|
| 14. | OGJCT | 76,75 |
|
| 15. | EPKolivargran.cat | 76,25 |
|
| 16. | OG-QCT | 75,75 |
|
| 17. | llucv2015 | 74 |
|
| 18. | Elena_GG | 73 |
|
| 19. | Hana | 71,25 |
|
| 20. | cgimenez1986 | 70,75 |
◌
◌
◌
◌
|
| 21. | NekoAkimori | 68 |
|
| 22. | Alejandro_GH | 67,25 |
|
| 23. | IgnacioA.Carranza | 65,75 |
◌
◌
|
| 24. | mon | 64,75 |
◌
◌
|
| 25. | MireiaWang | 64 |
|
| 25. | sonia_gumbau | 64 |
◌
|
| 27. | Truita_de_patata | 63,75 |
◌
|
| 28. | SMMolivargran | 62,5 |
◌
|
| 29. | GB_010 | 62,25 |
|
| 30. | Waribal072 | 62 |
|
| 31. | Lizzy | 60,75 |
◌
◌
◌
◌
◌
|
| 32. | Pauventus | 59,5 |
|
| 33. | leonor | 58 |
|
| 34. | Engelbert | 57 |
|
| 35. | Piperan78 | 49,75 |
◌
◌
◌
|
| 36. | Mitsuko.Baldeón.Higa | 48,25 |
◌
|
| 37. | Gumorm | 47,25 |
◌
|
| 37. | Naia_Azañedo | 47,25 |
|
| 39. | RamonCanet | 45 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 40. | nil.urbano | 42,25 |
|
| 41. | DNC | 37,75 |
◌
|
| 42. | Oriol47 | 34,75 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 43. | Kevin | 31,75 |
◌
◌
◌
◌
◌
◌
|
| 44. | JaviVilaseca | 28,75 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 45. | Mirambel | 28,25 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | Antaviana | 100 |
|
| 1. | JUANMA05@madina | 100 |
|
| 1. | MarionaT | 100 |
|
| 1. | Z99 | 100 |
|
| 5. | Asmaa-Laaraj-Zouba15 | 95 |
|
| 6. | _MartinÈliaaa_ | 94 |
|
| 6. | rodrigobustosñoñi@madina | 94 |
◌
|
| 8. | @adam. | 93 |
|
| 9. | Sergey | 92,75 |
|
| 10. | leonardogilabert | 92 |
|
| 11. | Pau_Bennasar_Cornelius_331_Mayor@madina | 88,25 |
|
| 12. | baianna | 87 |
|
| 13. | MONTSERRAT_GALAN | 86 |
|
| 14. | morgan | 85,75 |
|
| 15. | albaaguirre3 | 85,5 |
|
| 16. | TAMA | 82,25 |
|
| 17. | ilham | 82 |
◌
|
| 18. | geometrikos | 81,75 |
|
| 18. | JavierS | 81,75 |
|
| 20. | andreuoliver_013_@madina | 80,5 |
◌
|
| 20. | Sergiperelló@madina | 80,5 |
|
| 22. | MarwaSemmane0 | 78 |
◌
|
| 23. | THE_BOSS | 76,75 |
|
| 24. | OG_123 | 76,25 |
|
| 25. | NuriaOlaizola@madina | 75 |
|
| 26. | erimenrod | 72,5 |
|
| 26. | pbages | 72,5 |
|
| 28. | telmaa | 71,5 |
|
| 29. | laia2011 | 70,75 |
◌
|
| 30. | Kubra | 69,25 |
|
| 31. | MariaV | 68 |
◌
◌
◌
|
| 32. | Zihan_hoja | 65,5 |
◌
|
| 33. | Joel.Verdicht.Thanos@madina | 65,25 |
◌
|
| 34. | avrbondur | 62 |
◌
◌
|
| 35. | noesotgin | 61,75 |
◌
|
| 36. | Nizarrrr | 61 |
|
| 36. | SamuelPiñeiro | 61 |
|
| 38. | Nil-RG | 60,75 |
|
| 39. | PolPumarola | 60 |
|
| 40. | OGDSS | 58,75 |
|
| 41. | 1K3RVIII | 58,5 |
|
| 42. | Lluc_Villena | 57,5 |
|
| 43. | danielafz2011 | 56,25 |
◌
◌
◌
◌
|
| 44. | 2311@+-_14 | 53,25 |
|
| 45. | Oscar_romero | 50 |
|
| 46. | miriaam | 47,75 |
|
| 47. | Gajato | 47,25 |
◌
|
| 48. | Maial | 45,75 |
◌
◌
◌
◌
|
| 49. | Hugoruizperez | 43,25 |
◌
◌
◌
◌
◌
◌
◌
◌
|
| 50. | JúliaIris | 41,75 |
◌
|
| 51. | alexcj | 41 |
|
| 51. | julvidklo | 41 |
◌
|
| 53. | Niko | 39,5 |
|
| 54. | pauviltabernber | 38 |
|
| 55. | serpelcas@vila-roma.cat | 37 |
|
| 56. | Manuel13 | 36,5 |
◌
|
| 57. | LaraibIqbalNoreen@madina | 32,25 |
◌
◌
|
| 58. | Mehdi_prime | 18,75 |
◌
◌
◌
|
Llegenda
→ Resposta correcta
→ Resposta correcta més ràpida de la taula (+1 punt)
→ Resposta incorrecta


