Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.
Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.
Els problemes d'aquesta contrarellotge els han proposat l'Abel Doñate i l'Oriol Baeza, amb l'edició de Víctor López i les correccions de Cristian Reyes i Miquel Vilà.
Problema 1
3 punts
1 min
30 s
3 punts
•
1 min
30 s
La suma de tres nombres consecutius és un quadrat perfecte.
Quin és el mínim valor possible del major dels tres nombres?
La suma de tres nombres consecutius és: $$(n-1)+n+(n+1)=3n$$
El nombre de la forma $3n$ més petit que és un quadrat perfecte és: $$3n=3\times3 =3^2= 9$$
Si $n=3$, el major dels tres nombres és $n+1=\boxed4$.
Problema 2
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Un rectangle té perímetre $50 \text{ cm}$ i un costat fa $15 \text{ cm}$.
Quina és l’àrea en $\text{cm}^2$?
Anomenem $a,b$ els costats diferents del rectangle, i sabem que $a=15$.
El perímetre del rectangle és: $$\text{perímetre} = 2a + 2b = 2\cdot15+2b = 30+2b = 50$$
Només ens cal aïllar $b$: $$2b = 50 - 30 = 20 \quad\implies\quad b = \frac{20}2 = 10$$
Per tant, l’àrea del rectangle és: $$A_\text{rectangle} = a\cdot b = 15\cdot10 = \boxed{150 \text{ cm}^2}$$

Problema 3
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Per tal que $n^2$ sigui un cub perfecte, necessitem que $n$ ja sigui un cub perfecte (multiplicar el seu exponent per $2$ no farà que el nou exponent sigui un múltiple de $3$).
De la mateixa manera, per tal que $n^3$ sigui un quadrat perfecte, necessitem que $n$ sigui un quadrat perfecte.
El menor nombre que és alhora un quadrat perfecte i un cub perfecte és $2^6$ (la menor base possible, $2$, i el menor exponent possible que és alhora múltiple de $2$ i de $3$).
Així, la solució és $2^6=\boxed{64}$.
Problema 4
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Un centpeus vol pujar a un arbre. Pel dia és capaç de grimpar $5$ metres, però a la nit, mentre dorm, baixa $2$ metres.
Si l'arbre té una alçada de $50$ metres, quants dies trigarà el centpeus a arribar a dalt de tot?
En $15$ dies (i nits) ha fet $45 = 15\times (5-2)$ metres.
L'endemà fa els $5$ metres restants. Per tant, la solució és $\boxed{16}$ dies.
Problema 5
3 punts
1 min
30 s
3 punts
•
1 min
30 s
L’any vinent el Joan tindrà el doble d’anys que la Paula, però fa $5$ anys en tenia el triple.
Quants anys té el Joan?
Anomenem $x$ els anys de Joan i $y$ els anys de Paula respectivament.
Si l’any vinent el Joan tindrà el doble d’anys que la Paula: $$x+1 = 2(y+1) \quad\implies\quad x + 1 = 2y + 2 \quad\implies\quad x = 2y +1$$
Si fa $5$ anys en tenia el triple: $$x-5 = 3(y-5) \quad\implies\quad x-5=3y-15 \quad\implies\quad x = 3y-10$$
Substituïm la $x$ per trobar $y$: $$3y-10=2y+1 \quad\implies\quad y=1+10=11$$
I ara podem trobar la $x$: $$x = 2y+1 = 2\cdot11+1=22+1=23$$
I veiem que el Joan té $\boxed{23}$ anys.
Problema 6
4 punts
3 min
4 punts
•
3 min
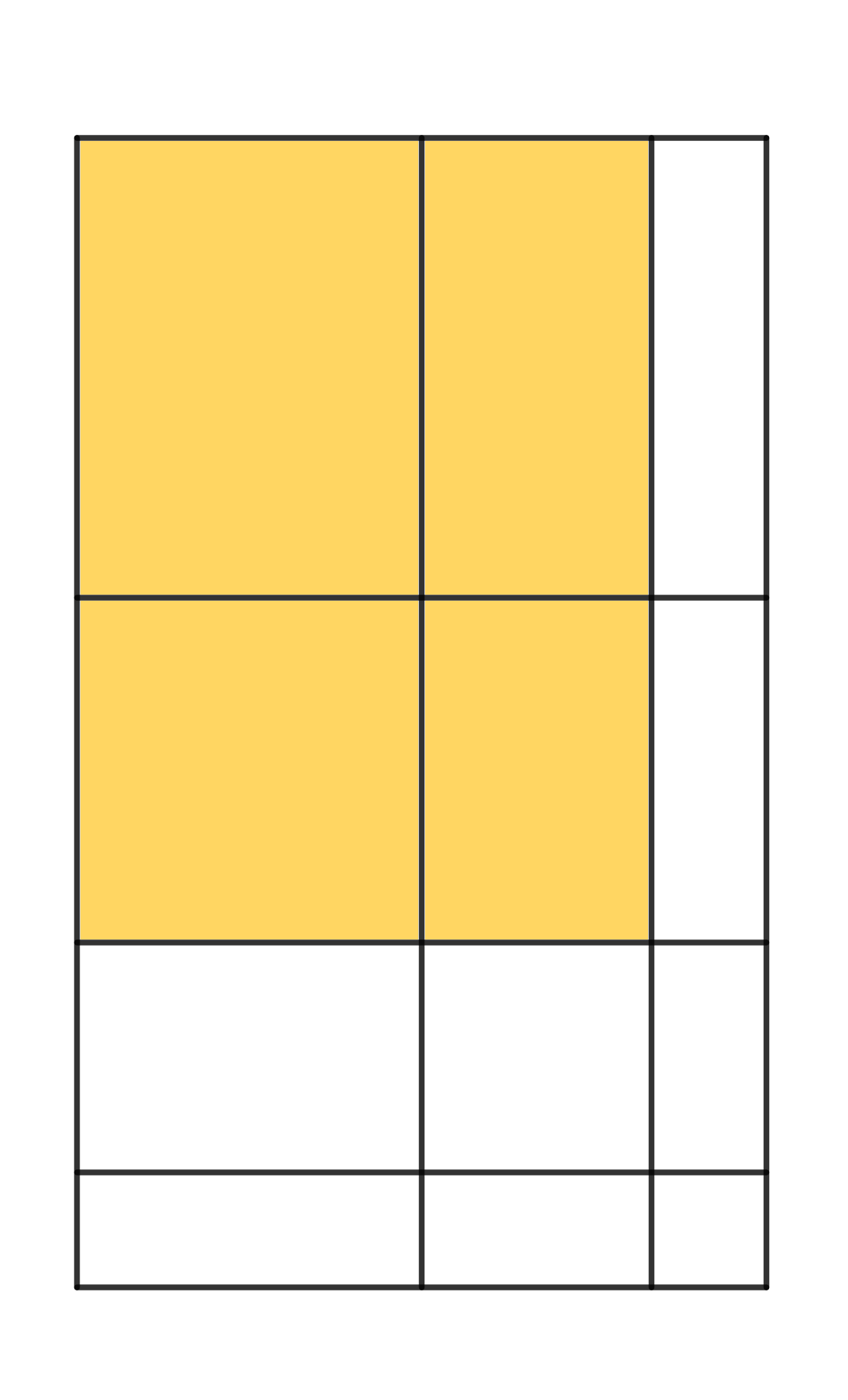
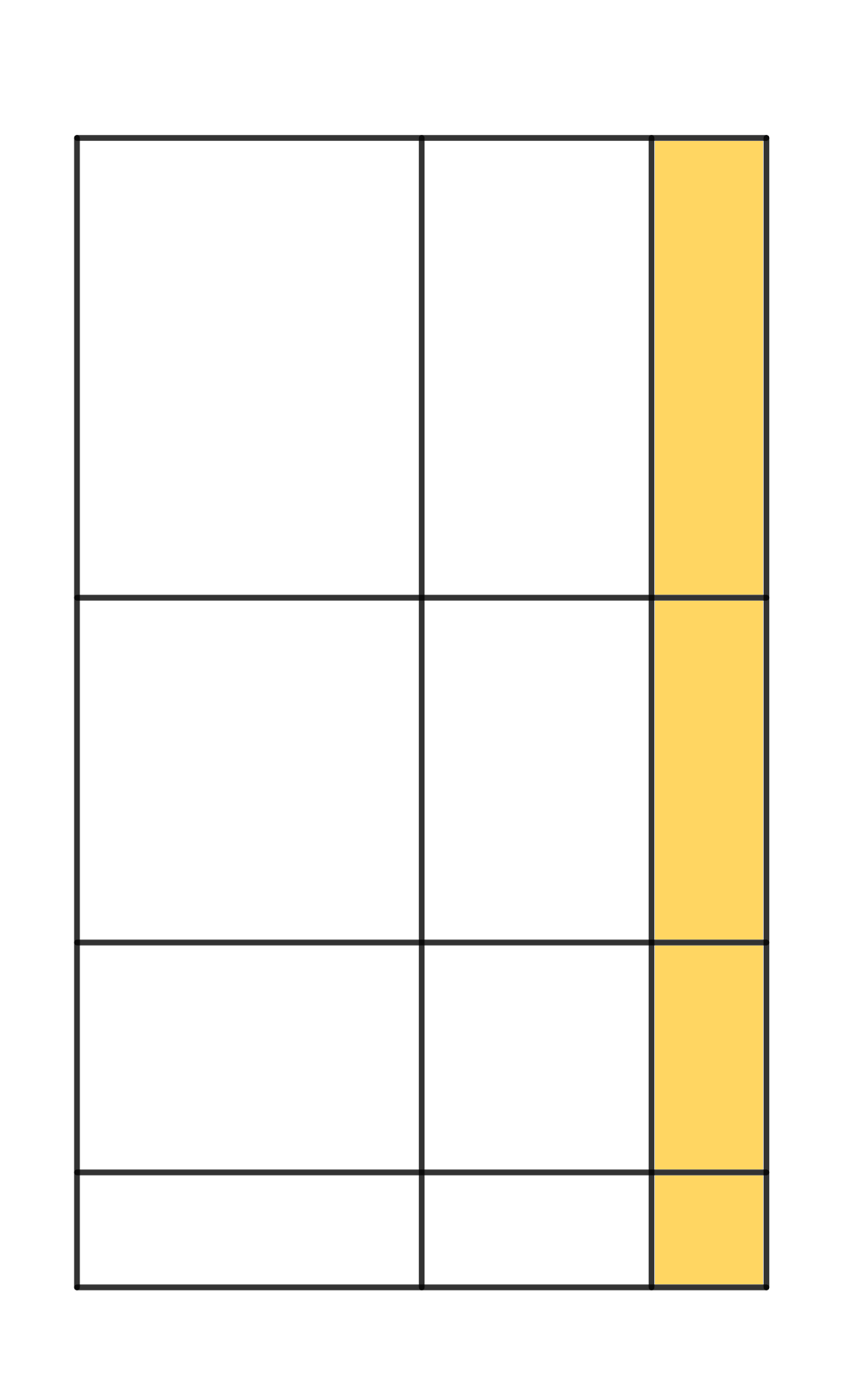
En un tauler $4 \times 3$, quants rectangles (de qualsevol mida, també quadrats) es poden comptar?

Per exemple:

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 7
4 punts
3 min
4 punts
•
3 min
Pau ha comprat per internet un dau trucat. Li han promès que amb aquest dau, la probabilitat de treure un $6$ és el doble que la de treure qualsevol altre resultat.
Quina és la probabilitat de treure un $6$, si els venedors diuen la veritat?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 8
4 punts
3 min
4 punts
•
3 min
En una reunió hi ha $10$ persones. Cada una dona la mà exactament a $3$ persones.
Quantes encaixades de mans hi ha hagut en total?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 9
4 punts
3 min
4 punts
•
3 min
En la figura següent tenim dos quadrats, el més gran amb àrea $2$. En color taronja, hi dibuixem un trapezi i un triangle.
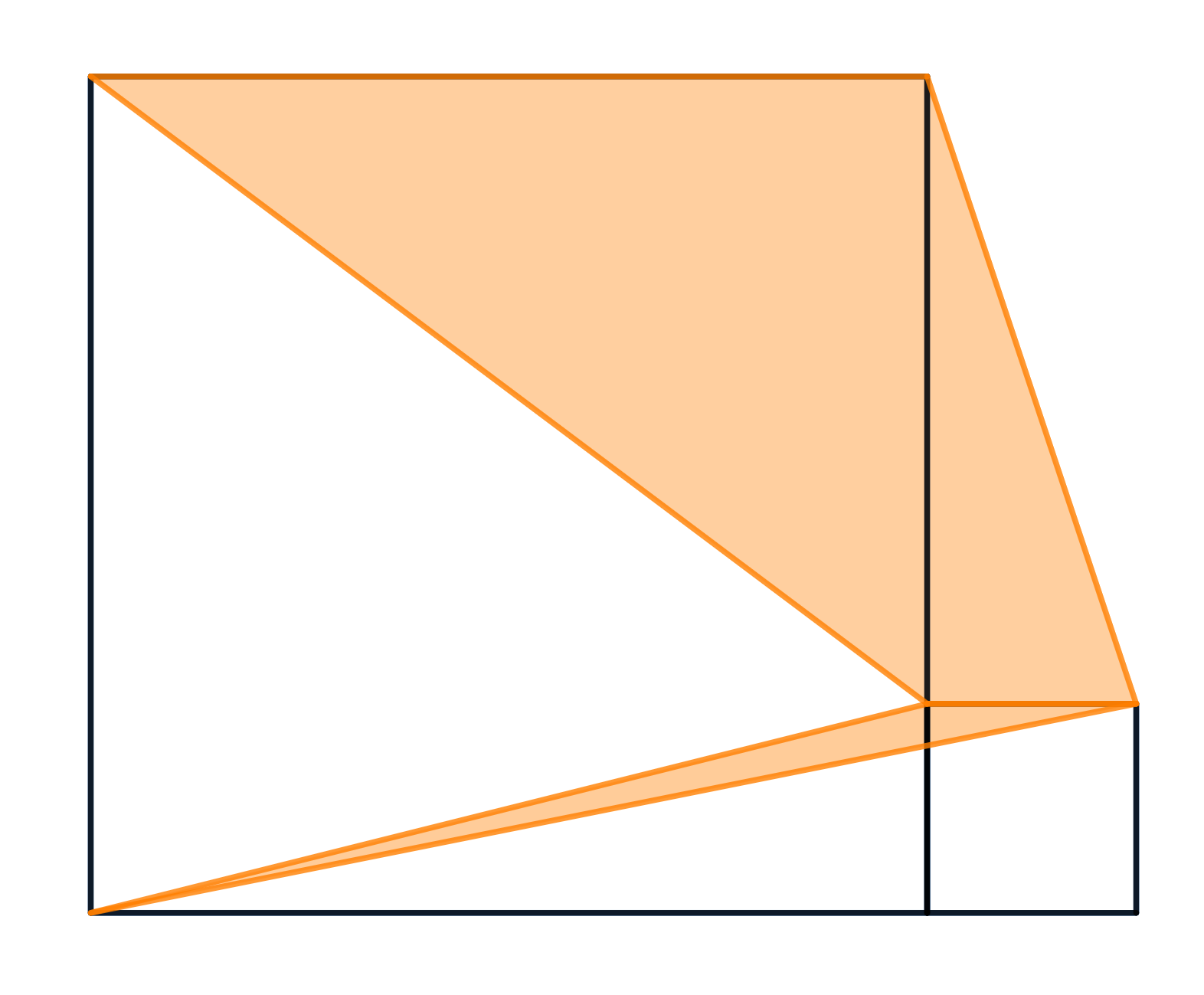
Quina és l'àrea d'aquests dos junts, indicada en color taronja?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 10
4 punts
3 min
4 punts
•
3 min
En un tauler $2\times 2$, volem acolorir cada quadrat de color blanc o negre. Direm que una coloració és «egarenca» si el nombre de quadrats negres és parell.
Per exemple, aquests són exemples de coloracions egarenques:

Quantes coloracions egarenques hi ha?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 11
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Sigui $S$ el conjunt $\{1,2,3,4,5,6,7,8\}$. Diem que un subconjunt és «especial» si el nombre d’elements és igual al menor dels elements del subconjunt.
Per exemple, el $\{3,5,7\}$ és especial. Quants subconjunts especials té $S$?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 12
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Tenim un tauler de $5\times5$ caselles inicialment blanques. La Clàudia vol pintar de verd $N$ caselles, on $N$ és el seu número preferit. S'adona que, independentment de quines $N$ caselles d’entre les $25$ possibles triï per pintar, sempre hi haurà una fila o una columna o una diagonal amb almenys tres caselles verdes. Quin és el mínim valor possible de $N$?
Un exemple d'un tauler on no hi ha cap fila, columna o diagonal amb almenys tres caselles verdes.

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 13
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Considerem la següent figura on l'àrea blanca és $62.5$.
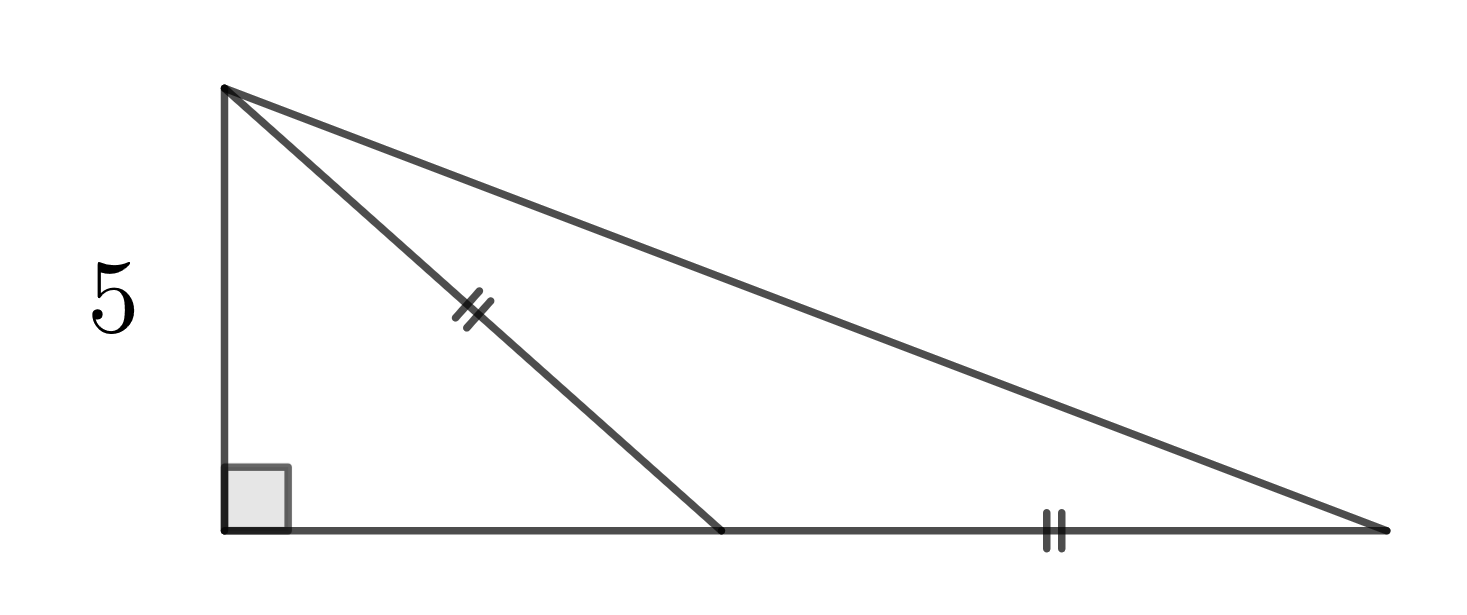
Quant mesuren els costats marcats amb dues ratlles?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 14
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Tenim un nombre de dues xifres $M$ el multipliquem per $4$, sumem els dígits del resultat obtingut, i resulta que recuperem el nombre original $M$.
Quin és aquest nombre $M$?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 15
5 punts
4 min
30 s
5 punts
•
4 min
30 s
En una capsa hi ha $6$ boles numerades de l’$1$ al $6$, i les anem traient, una a una, sense mirar.
Quantes boles hem de treure, com a mínim, per estar segurs que la suma és un múltiple de $3$?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Concurs 4t d'ESO
Estudiants que cursen 4t d'ESO o un curs inferior.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | Starpot | 86 |
|
| 2. | bruno_algaba | 79,25 |
|
| 3. | Cristian_García | 76,75 |
◌
|
| 4. | Montse2011 | 76,5 |
|
| 5. | Xpro02272 | 74,25 |
|
| 6. | Elena_GG | 72 |
|
| 7. | M461 | 71,75 |
|
| 8. | Kalajary27 | 69,25 |
|
| 9. | Hana | 69 |
|
| 9. | leonardogilabert | 69 |
|
| 11. | IgnacioA.Carranza | 67,25 |
◌
◌
|
| 11. | RogerC | 67,25 |
|
| 13. | MireiaWang | 66,25 |
◌
◌
◌
|
| 14. | PauMartínezSánchez | 65 |
|
| 15. | b.baraaazz | 64 |
|
| 16. | carlit | 63 |
|
| 16. | Marc25 | 63 |
|
| 18. | YoussefelGazouliMachate | 62,25 |
|
| 19. | NekoAkimori | 61,75 |
|
| 20. | Pmava | 60,5 |
|
| 21. | martiruealgado | 59,5 |
◌
◌
◌
◌
|
| 22. | Antaviana | 58,5 |
|
| 23. | Milena_Arsenyan | 56,75 |
◌
◌
|
| 24. | ArnauEPB | 56,25 |
|
| 25. | Lluc_Villena | 52,25 |
|
| 26. | GB_010 | 51,5 |
|
| 26. | Mitsuko.Baldeón.Higa | 51,5 |
◌
◌
|
| 28. | sonia_gumbau | 49,75 |
|
| 29. | Carmortilla | 49,5 |
◌
|
| 30. | MartíP | 49,25 |
|
| 30. | Truita_de_patata | 49,25 |
◌
◌
◌
◌
◌
◌
◌
|
| 32. | Edna | 46 |
◌
|
| 32. | Marwaabarkan@ | 46 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 34. | Naia_Azañedo | 45,5 |
◌
|
| 35. | Albert_.Gimenez | 45 |
◌
◌
◌
◌
|
| 36. | isaac | 44,75 |
◌
◌
|
| 36. | Lina | 44,75 |
◌
|
| 36. | Origamer | 44,75 |
◌
◌
◌
◌
◌
◌
|
| 39. | NinaRuzCárceles | 42,75 |
◌
|
| 40. | Sergiosierra_99 | 41 |
|
| 41. | GUGI | 40,75 |
|
| 42. | Pir2 | 40,5 |
◌
|
| 43. | GuiuT | 40,25 |
◌
|
| 44. | Pepnastic | 40 |
◌
◌
◌
◌
◌
◌
◌
|
| 45. | zegui14 | 39,75 |
◌
◌
|
| 46. | sofia1234 | 39,25 |
|
| 47. | Daniela.Ruiz. | 38,5 |
◌
◌
◌
◌
◌
|
| 48. | Alexgonzalvo | 38,25 |
◌
◌
◌
◌
|
| 49. | GameKnight_999 | 36,5 |
◌
◌
|
| 50. | leonor | 35,5 |
◌
◌
◌
◌
◌
|
| 51. | diegosolegomez | 33,25 |
|
| 51. | Paulaaavelascoo | 33,25 |
◌
|
| 53. | DidicG | 30 |
◌
◌
◌
|
| 54. | wiam | 28,5 |
◌
◌
|
| 55. | Lia | 28 |
◌
◌
◌
|
| 56. | Origami2.0 | 24,75 |
|
| 57. | LauraSaezMC | 22,75 |
◌
|
Concurs obert
Usuaris que han superat 4t d'ESO, professors, etc.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | arakelov | 90 |
|
| 2. | Giselavallejos.__ | 84 |
|
| 3. | Omar_Bakkouh | 83 |
|
| 4. | Ian_Adria | 81 |
|
| 5. | OG_JAP | 80,75 |
|
| 5. | OGNHGPKMN | 80,75 |
|
| 7. | OGJCT | 78,75 |
|
| 8. | OG-QCT | 76,75 |
|
| 9. | OGWHH | 74,75 |
|
| 10. | eva.pascual | 73,75 |
|
| 11. | Lluis_Carrasco | 73,25 |
|
| 12. | lluc.galindo | 72,75 |
◌
|
| 13. | cgimenez1986 | 70,75 |
|
| 14. | MCuadros | 67,75 |
|
| 15. | Frogrammer | 67,25 |
◌
|
| 16. | SMMolivargran | 66,75 |
|
| 17. | Maribel | 62,75 |
|
| 18. | DNC | 62 |
|
| 19. | OG-HBJ | 60,5 |
◌
◌
◌
◌
◌
|
| 20. | EPKolivargran.cat | 59,5 |
|
| 21. | nicoo_.67 | 58 |
|
| 22. | estel | 54,5 |
◌
◌
◌
|
| 23. | mon | 43,75 |
◌
◌
◌
◌
◌
◌
◌
◌
|
| 24. | RiuEgipte | 37 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 25. | VA | 35,5 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 26. | Oriol47 | 31 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 27. | Edgar | 26,5 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | Adam12 | 99 |
|
| 2. | Mateu_BC | 72,75 |
◌
|
| 3. | geometrikos | 71 |
◌
◌
|
| 4. | Who | 70,5 |
|
| 5. | OG_123 | 69,5 |
|
| 6. | VíctorP | 68,75 |
|
| 7. | sumjulianmejia7 | 67,5 |
|
| 8. | Gerard28 | 63,25 |
◌
|
| 9. | hhxrayy | 61 |
|
| 10. | Tbspro | 49 |
|
| 11. | SonGoku | 45,5 |
◌
◌
◌
◌
◌
◌
|
Llegenda
→ Resposta correcta
→ Resposta correcta més ràpida de la taula (+1 punt)
→ Resposta incorrecta


