Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.
Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.
Els problemes d'aquesta contrarellotge els han proposat l'Abel Doñate i l'Oriol Baeza, amb l'edició de Víctor López i les correccions de Cristian Reyes i Miquel Vilà.
Problema 1
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Recordem que cada nombre enter té una descomposició única en factors primers.
A la dreta, tenim $10^k = 2^k \cdot 5^k$. D’altra banda, a l’esquerra podem agrupar els factors com $$ 5\cdot 2 \cdot 4 \cdot 8 \cdot 5 \cdot 5 \cdot 5 \cdot 5 \cdot 5 = 5\cdot 2^1 \cdot 2^2 \cdot 2^3 \cdot 5^5 = 2^6 \cdot 5^6 $$
Aleshores, de la igualtat en la descomposició, tenim necessàriament que $\boxed{k=6}$.
Problema 2
3 punts
1 min
30 s
3 punts
•
1 min
30 s
D’entrada, hem de comptar els múltiples de $63$ que estiguin entre $500$ i $700$ que no siguin parells.
Podem ubicar fàcilment un múltiple de $63$ en aquest rang: el $630=63\cdot 10$. Aquest no és senar, així que no comptarà per la suma que ens interessa, però ens serveix per trobar els altres múltiples de $63$ senars en el rang $500$ i $700$.
Partint del $630$, restant $63$ cap avall, trobem el $567$ i després el $504$, i el següent ja està per sota de $500$ així que no ens interessa. D’aquests dos que hem trobat, només ens quedarem amb el $567$ perquè volem nombres senars.
Ara cap amunt, partint del $630$ i sumant $63$, trobem el $693$, i el següent ja seria per sobre de $700$ així que no ens interessa.
Tot plegat, els números que volíem trobar són el $567$ i el $693$, i la seva suma és $\boxed{1260}$.
Problema 3
3 punts
1 min
30 s
3 punts
•
1 min
30 s
En un mini tauler d’escacs de $4 \times 4$, quants reis poden col·locar-se de manera que no s’ataquin entre ells?
Per exemple, si col·loquem un rei com a la següent figura, no en podem col·locar cap altre a les caselles ratllades en vermell:
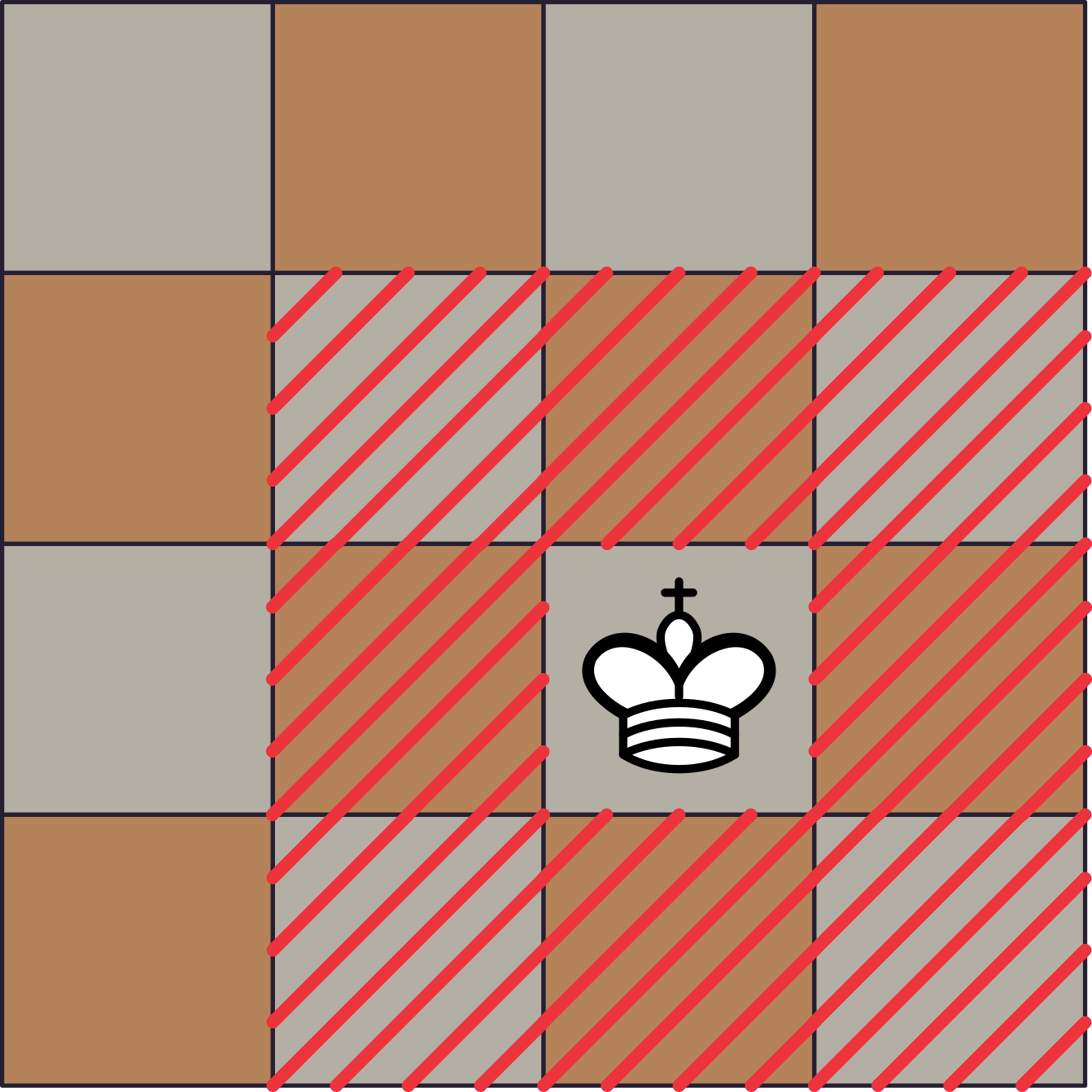
Primer de tot, recordem que els reis ataquen a les $8$ caselles adjacents a la que es troben. Vegem que podem col·locar $4$ reis, però que $5$ ja no.
La idea per a veure les dues qüestions que cal demostrar és la mateixa: subdividir el tauler en blocs de $2\times 2$, que en són exactament $4$.
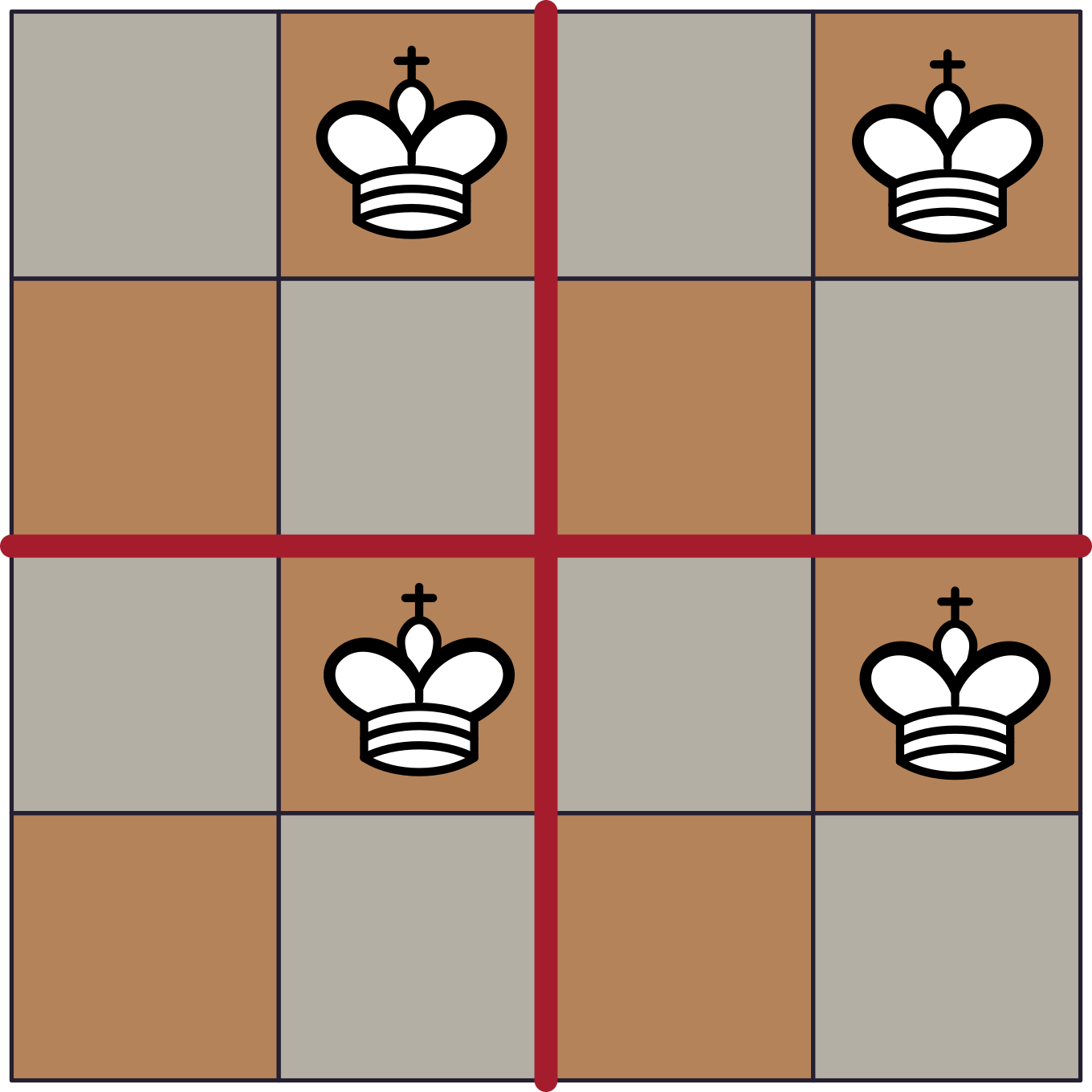
Si col·loquem un rei en la cantonada superior dreta de cada un d’aquests blocs, aconseguim posar $4$ reis que no s’ataquen entre ells.
Encara més, suposem que poguéssim posar $5$ reis. Pel principi del colomar, veiem que hi haurà un d’aquests blocs $2\times2$ amb dos reis. Però això és impossible, ja que aleshores aquests dos s’estarien atacant entre ells.
Tot plegat, la resposta és $\boxed{4}$.
Problema 4
3 punts
1 min
30 s
3 punts
•
1 min
30 s
L'Oriol té dos nombres enters preferits $a,b$, però no ens vol dir quins són. Només ens ha volgut explicar que $a+b=7$ i que $a^2 + b^2 = 29$.
Si $a$ és el petit dels dos ($a \leq b$), quant val $a$?
Volem resoldre el següent sistema $$ \begin{cases} a+b = 7 \\ a^2 + b^2 = 29 \end{cases}$$
La manera més elegant de resoldre'l és elevar al quadrat la primera equació, i al resultat substituir-hi la segona $$ (a+b)^2 = 49 \quad \implies \quad a^2 + b^2 + 2ab = 49 \quad \implies \quad 29 + 2ab = 49 \quad \implies 2ab = 20$$
Aleshores, el sistema resulta en $$ \begin{cases} ab = 10 \\ a+b = 7 \end{cases}$$
Provant valors, podem veure que $(a,b)=(2,5)$ és una solució. Tanmateix, anem a justificar bé com resoldre aquest sistema.
Solució 1
Una possibilitat és intentar trobar quant val $a-b$. Per això, primer trobem el seu quadrat, ja que $$(a-b)^2 = a^2 + b^2 -2ab = 29 - 20 = 9 \quad \implies \quad a-b = \pm 3 $$
Encara més, com que estem assumint que $a \leq b$, tenim que $a-b \leq 0$ és negatiu, per tant, concloem que $a-b = -3$. Tot plegat, combinant les equacions $$ \begin{cases} a-b = -3 \\ a+b = 7 \end{cases} \quad \implies \quad \begin{cases} 2a = 4 \\ 2b = 10 \end{cases} $$
És a dir, $\boxed{(a,b) = (2,5)}$.
Solució 2
Una altra manera de resoldre l'últim sistema, inspirada per les relacions de Cardano-Viète, és considerar el següent polinomi de grau $2$, que té arrels $a$, $b$ $$ (x-a)(x-b) = x^2 - (a+b)x + ab = x^2 - 7x + 10 $$
Per tant, resolent aquest polinomi amb la fórmula per a equacions de segon grau $$ x = \frac{7 \pm \sqrt{7^2 - 4 \cdot 10 }}{2} = \frac{7 \pm 3}{2} = \begin{cases} 2 \\ 5 \end{cases}$$
És a dir, les arrels del polinomi, i per tant els valors que cerquem, són $\boxed{(a,b) = (2, 5)}$.
Problema 5
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Trobeu l’enter positiu $n$ més petit tal que $2025n$ i $\frac{2025}{n}$ siguin potències quartes (és a dir, són $m^4$ per algun enter positiu $m$).
Nota: Recorda que $2025 = 3^4 \cdot 5^2$.
Primer de tot, considerem la descomposició en factors primers $2025 = 45^2 = 3^4 \cdot 5^2$. També, recordem que per tal que un nombre sigui una potència quarta cal que tots els exponents en la seva descomposició en factors primers siguin múltiples de $4$.
Aleshores, perquè $2025n$ sigui potència quarta, ens cal com a mínim que $n$ tingui un factor $5^2$.
Prenent el mínim possible $n = 5^2 = 25$, veiem que $2025n = 3^4 \cdot 5^4$, però també $\frac{2025}{n} = 3^4$, així que la resposta és $\boxed{25}$.
Problema 6
4 punts
3 min
4 punts
•
3 min
Tenim un hexàgon regular de costat $1$. Dels $6$ possibles vèrtexs en triem $3$, i els unim dibuixant un triangle.
Quin és el màxim perímetre que pot tenir aquest triangle?
Per exemple, aquesta és una possibilitat:
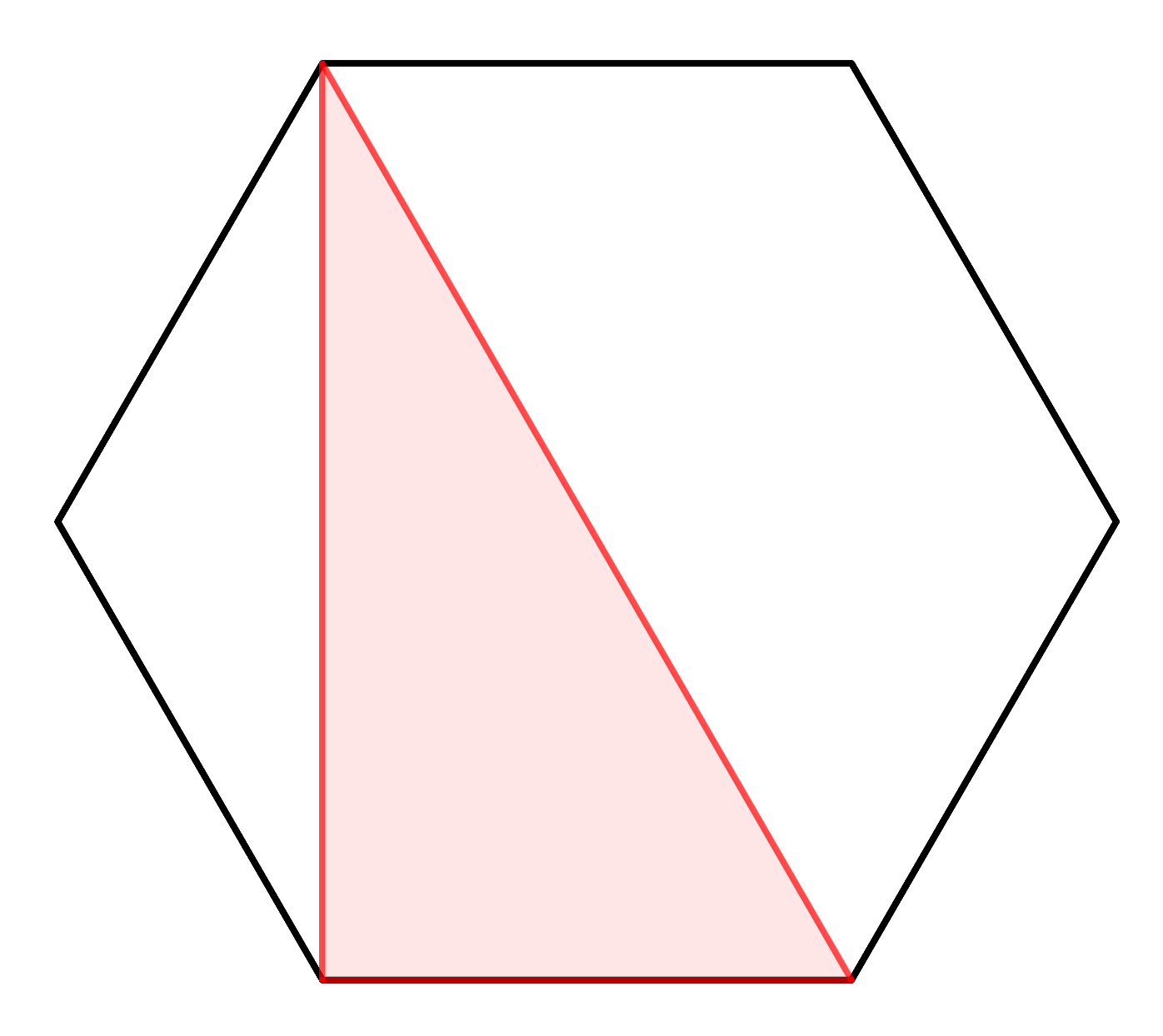
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 7
4 punts
3 min
4 punts
•
3 min
Quants triangles diferents de perímetre $7$ es poden aconseguir amb costats naturals (és a dir, enters positius)?
Nota: Considereu que dos triangles són el mateix si són iguals després de rotacions o simetries.
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 8
4 punts
3 min
4 punts
•
3 min
Tenim en una bossa els dígits $\{1, 2, 3, 4\}$ i volem formar números usant tots els dígits en algun ordre. Quants números podem formar que siguin múltiples de $9$?
Per exemple, el número $1234$ utilitza tots els dígits, però no és múltiple de $9$.
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 9
4 punts
3 min
4 punts
•
3 min
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 10
4 punts
3 min
4 punts
•
3 min
Escrivim un nombre de $2$ xifres tal que d’esquerra a dreta les xifres estan ordenades de major a menor (per exemple, el $32$). A aquest nombre, li restem el nombre obtingut en invertir l’ordre de les xifres (per exemple, de $32$ obtenim $23$, i la resta dona $32-23 = 9$).
Quina és la suma de tots els números que podem obtenir com a resultat?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 11
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 12
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Dintre d’un quadrat $ABCD$, triem un punt $P$, i denotem les àrees dels triangles que es formen $[APB] = S_1$, $[BPC] = S_2$, $[CPD] = S_3$, $[DPA] = S_4$, tal com es veu al dibuix.
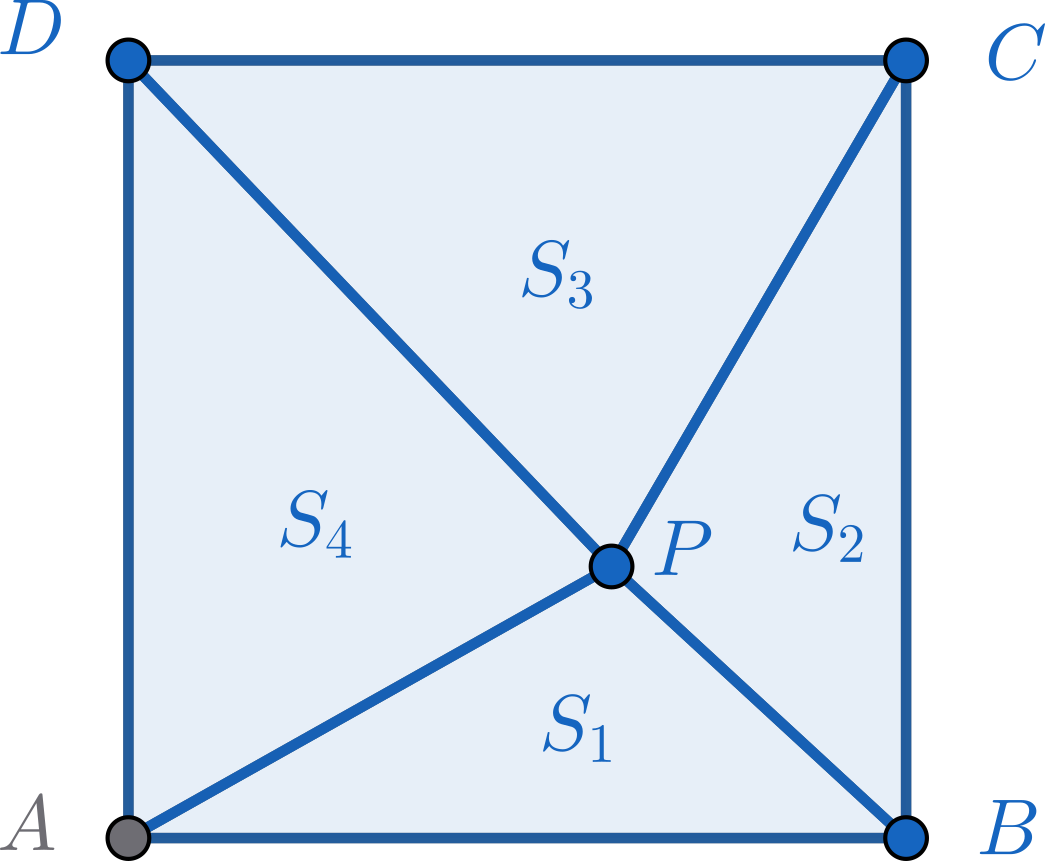
Si tenim que $S_1^2 + S_2^2 = S_3^2 + S_4^2$, quin és l’angle $\angle PAB$?
Nota: Pots assumir que les coordenades dels punts són $A=(0,0), B=(1,0), C=(1,1), D=(0,1)$ i $P=(x,y)$.
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 13
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Pista: Què passa si sumem totes les equacions?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 14
5 punts
4 min
30 s
5 punts
•
4 min
30 s
L’Abel té dues funcions preferides: $$f(x) = ax + b$$ $$g(x) = bx + a$$ On $a,b$ són enters positius.
La seva professora de matemàtiques li ha fet notar una propietat molt interessant sobre les seves funcions preferides, i és que resulta que $f(g(x)) = g(f(x))$ per a tot $x$.
Quant ha de valer la quantitat $a-b$?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 15
5 punts
4 min
30 s
5 punts
•
4 min
30 s
El polinomi $P(x)=x^3 - 21 x^2 + k x - 216$ té $3$ arrels que formen una progressió geomètrica. Quin és el valor de $k$?
Pista: Recorda que, si diem $\alpha,\beta,\gamma$ a les arrels en qüestió, tenim $P(x) = (x-\alpha)(x-\beta)(x-\gamma)$. Expandint aquest producte, podrem comparar els coeficients del polinomi amb expressions involucrant les arrels.
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Concurs 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat o un curs inferior.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | Gabriel2873 | 92 |
|
| 2. | Yanis | 86 |
|
| 3. | sugaaah | 84 |
|
| 4. | danidelrio | 83 |
|
| 5. | PauMR | 82,25 |
|
| 6. | Aleix_Berenguer | 81,75 |
|
| 7. | claudia.galera | 81,25 |
◌
|
| 7. | Danna_Munoz | 81,25 |
◌
|
| 9. | Iman.marzak | 80,25 |
|
| 10. | MartinaPla | 79,75 |
|
| 11. | Xavier_Martí_Rosell | 79 |
|
| 12. | inas | 78,75 |
|
| 13. | isabelzhu | 77,5 |
|
| 14. | danicharles | 77 |
|
| 15. | Jiapengwang | 76,5 |
|
| 16. | biel.astals | 76 |
◌
|
| 16. | CosinusExpansionEnjoyer12 | 76 |
|
| 18. | txell_polo | 75,25 |
◌
◌
|
| 19. | Deivi | 73 |
|
| 20. | paupi3 | 72,75 |
|
| 21. | eva.pascual | 72 |
|
| 22. | Jan_Bacardit_Díaz | 71,5 |
|
| 23. | Starpot | 71,25 |
|
| 24. | Frogrammer | 70 |
◌
◌
◌
|
| 24. | Oana | 70 |
◌
|
| 26. | Lluc_Ferrer | 69,75 |
|
| 26. | Omar_Bakkouh | 69,75 |
|
| 28. | @NourDiallo.0 | 69,5 |
◌
|
| 29. | AndreiMatematic | 69,25 |
|
| 29. | Marta.Alsina | 69,25 |
|
| 31. | Ian_Adria | 69 |
◌
◌
|
| 32. | AinaGL | 68,5 |
|
| 33. | Brega | 68 |
◌
◌
◌
◌
◌
◌
|
| 34. | l.elkhamlichi | 67,5 |
◌
|
| 34. | Yasmine_menqar | 67,5 |
|
| 36. | LlucB | 67 |
◌
|
| 36. | RogerC | 67 |
|
| 38. | Mariona_G | 66,75 |
◌
|
| 39. | basma.bhira | 66,5 |
◌
|
| 40. | marta123 | 66 |
◌
◌
◌
◌
◌
◌
|
| 41. | lluc.galindo | 65,75 |
|
| 42. | Iman09 | 65 |
◌
|
| 43. | EParedes | 64,5 |
|
| 44. | brianaa.boghian.9 | 64,25 |
|
| 44. | MarcFrasin | 64,25 |
|
| 46. | Bielo | 63,75 |
◌
◌
◌
|
| 46. | gerard_EPB | 63,75 |
◌
◌
◌
◌
◌
◌
|
| 48. | estel | 63,25 |
◌
|
| 49. | OG-HBJ | 63 |
|
| 50. | carlamunoz | 62,75 |
◌
|
| 51. | ivet.munoz | 62,5 |
◌
◌
|
| 51. | JanaVila | 62,5 |
◌
◌
|
| 51. | MarcSans | 62,5 |
|
| 54. | Amin-Benjalloul | 62,25 |
|
| 55. | Aortega1 | 62 |
|
| 55. | Emoncada08 | 62 |
◌
|
| 57. | AbrilGarciaEPB | 61,75 |
|
| 57. | ClaudiaMoyano | 61,75 |
|
| 57. | Mariarepullo | 61,75 |
◌
|
| 57. | OGNHGPKMN | 61,75 |
◌
|
| 57. | RiuEgipte | 61,75 |
◌
|
| 57. | TheNumberPie | 61,75 |
|
| 63. | claudia90002 | 61,5 |
◌
|
| 64. | SergioRiveroDiaz | 60,25 |
|
| 65. | Jangar | 59,75 |
|
| 66. | nico.L.S | 59,5 |
◌
◌
|
| 67. | OGWHH | 59 |
◌
|
| 68. | ariii | 58,75 |
◌
|
| 69. | leire.bernat | 58,5 |
◌
◌
|
| 70. | tea.montero | 57,25 |
◌
|
| 71. | FDLF | 57 |
|
| 72. | Mrnwz.g | 56,75 |
|
| 73. | CarolinaMolina | 56,5 |
|
| 74. | elzakri_23 | 55,75 |
|
| 75. | emma.garcia | 55 |
◌
|
| 76. | isaac | 54,75 |
◌
◌
◌
◌
|
| 76. | Laia_Alfonso | 54,75 |
◌
◌
◌
◌
◌
|
| 78. | claudiamiquel2009 | 54,25 |
|
| 79. | Laia.Macías | 53,75 |
|
| 80. | Paugc | 51,75 |
|
| 81. | Zihan_hoja | 51 |
◌
|
| 82. | alexsabateelordi | 49,75 |
◌
|
| 83. | OG-QCT | 49 |
◌
◌
◌
◌
◌
◌
◌
|
| 84. | Santiago.b | 46,75 |
|
| 85. | Edgar | 45,25 |
◌
|
| 86. | IrinaPla | 45 |
|
| 87. | Olivia | 44,75 |
|
| 88. | maria-10 | 44,5 |
|
| 89. | nil.urbano | 43,25 |
|
| 90. | Pir2 | 36,75 |
◌
|
| 91. | XinyueZhu | 36 |
|
| 92. | claudia_alonso_valenti | 34,5 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 93. | Yoichi | 33,25 |
◌
|
| 94. | mar_royoo | 31,25 |
◌
◌
◌
◌
◌
◌
◌
|
| 94. | ypan | 31,25 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 96. | Origami2.0 | 25 |
◌
|
Concurs obert
Usuaris que han superat 2n de Batxillerat, professors, etc.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | arakelov | 82 |
◌
◌
|
| 2. | dani97 | 66 |
◌
◌
|
| 3. | bernatromaniplafa | 63,5 |
◌
◌
|
| 4. | Carbassa | 62 |
|
| 5. | Maribel | 60 |
◌
◌
◌
◌
◌
|
| 6. | mon | 28 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | ZohmatiZhorroSky | 99 |
|
| 2. | _abril_pacho_ | 89 |
|
| 3. | uyiw22395 | 84 |
◌
|
| 4. | chiquibi | 81 |
|
| 5. | Gustavo | 79,75 |
|
| 6. | jllobera | 78,75 |
|
| 6. | OG_123 | 78,75 |
|
| 8. | geometrikos | 61,25 |
|
| 9. | marti+uriol | 58,25 |
|
| 10. | Sergey | 27,25 |
|
Llegenda
→ Resposta correcta
→ Resposta correcta més ràpida de la taula (+1 punt)
→ Resposta incorrecta


