Contrarellotge: hivern 2026 (2n d'ESO)
Diumenge, 8 de febrer de 2026 a les 19:00

Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.

Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Problema 1
3 punts   •   1 min 30 s

La Marta va cada dia a la cantina de l'institut a esmorzar. A la cantina hi ha dues opcions de beguda (suc i batut), i tres de menjar (croissant, empanada i entrepà). Com és molt indecisa, li agradaria provar totes les combinacions.

Quants dies trigaria a fer-ho, si cada dia tria una combinació nova?

A. $2$
B. $5$
C. $4$
D. $1$
E. $6$
En blanc
Mostra solució

El problema es redueix a trobar les combinacions de dos elements de dos conjunts de mida $2$ (beguda) i $3$ (menjar). Veiem que triar en el primer conjunt (beguda) i en el segon (dinar) és independent, per la qual cosa la quantitat de combinacions és el producte $2\times 3 = \boxed{6}$

Problema 2
3 punts   •   1 min 30 s

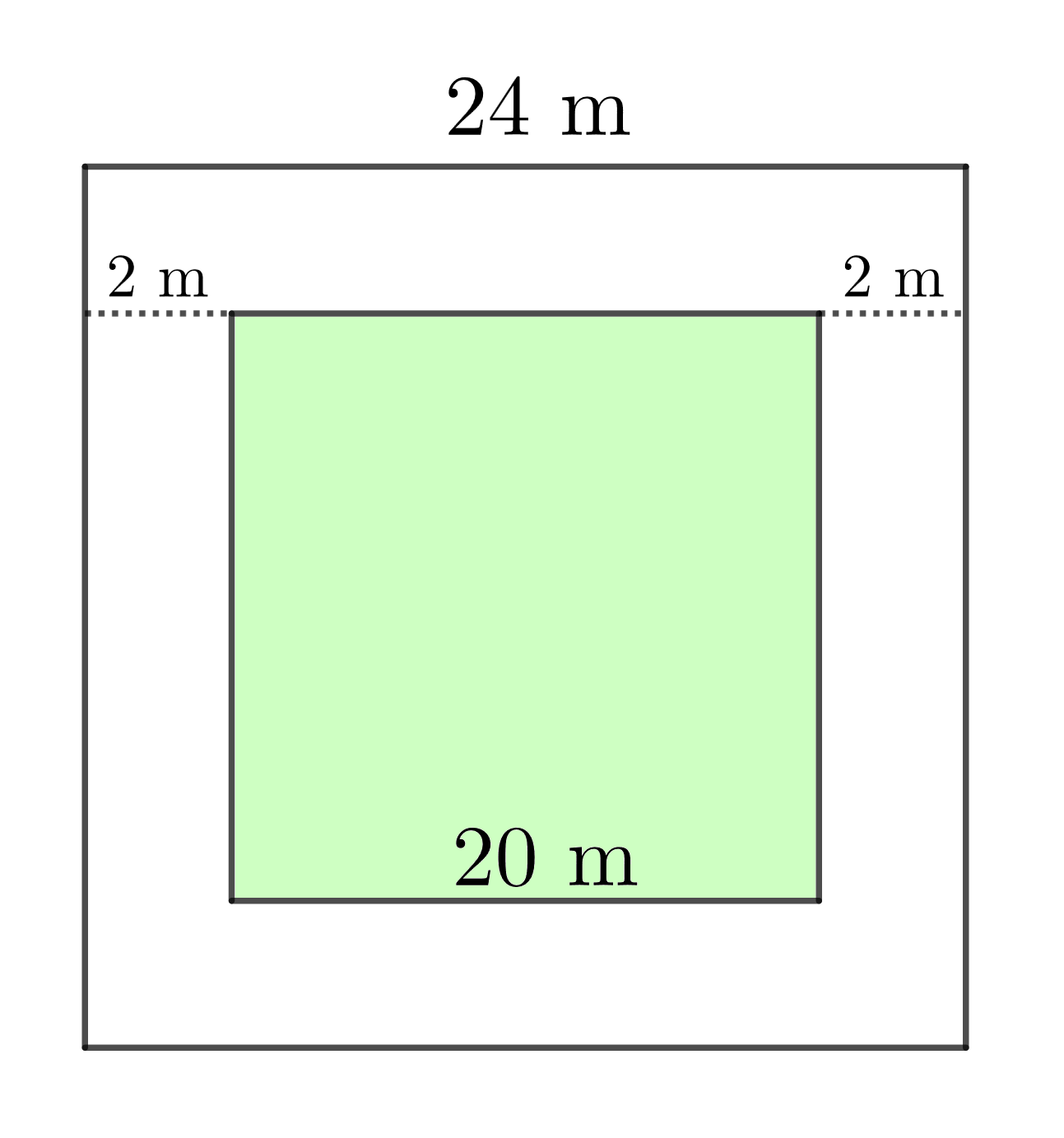
Un jardí quadrat té un costat de $24\text{ m}$. Es construeix un camí de pedra a l'interior, resseguint el perímetre per dins del quadrat. Si el camí té una amplada constant de $2\text{ m}$, quina és l’àrea de la zona de gespa que queda al centre?

A. $484 \text{ m}^2$
B. $324 \text{ m}^2$
C. $420 \text{ m}^2$
D. $400 \text{ m}^2$
E. $496 \text{ m}^2$
En blanc
Mostra solució

D’acord amb l’enunciat, el costat inicial del jardí és de $24\text{ m}$, però aleshores destinem $2\text{ m}$ a cada costat per al camí.

Per tant, el costat del jardí quadrat que roman dins el camí és de $24-2-2 = 20$ i llavors l’àrea demanada és $20\cdot 20 = \boxed{400 \text{ m}^2}$.

Problema 3
3 punts   •   1 min 30 s

La suma de tres nombres enters senars consecutius és $15$. Quin és el producte d'aquests tres nombres?

A. $67$
B. $15$
C. $105$
D. $81$
E. $315$
En blanc
Mostra solució

Diguem $x-2,x$ i $x+2$ als tres nombres senars consecutius. Aleshores, l’enunciat diu que

$$(x-2)+x+(x+2) = 3x = 15,$$

d’on deduïm que $x = 5$, i els tres nombres son $3,5$ i $7$. Per tant, el producte cercat és

$$3\cdot 5 \cdot 7 = \boxed{105}.$$

Problema 4
3 punts   •   1 min 30 s

La mitjana d’edat d’un grup de $5$ amics és de $16$ anys. Si marxa el més gran, que té $20$ anys, quina serà la nova mitjana d’edat dels $4$ amics restants?

A. $13$
B. $15$
C. $12$
D. $14$
E. $11$
En blanc
Mostra solució

Comptem quina era la suma total d’anys inicialment, que ha de ser $16 \cdot 5 = 80$.

Per tant, en marxar una persona de $20$ anys, les persones restants tenen una edat total de $80-20=60$ anys.

En particular, la mitjana dels 4 restants és $\frac{60}4 = \boxed{15}$ anys.

Problema 5
3 punts   •   1 min 30 s

Quants nombres capicua de $4$ xifres són múltiples de $5$?

Nota: Per exemple, $1221$ és capicua però no és múltiple de $5$.

A. $10$
B. $0$
C. $20$
D. $100$
E. $1000$
En blanc
Mostra solució

Primer de tot, notem que un nombre és múltiple de $5$ si, i només si, acaba en $0$ o $5$.

Tanmateix, com volem que sigui capicua, no podrà ser que la última xifra sigui $0$, perquè la primera no pot ser-ho. Per tant, ja tenim que el nombre ha d’acabar en $5$ i, per ser capicua, també comença per $5$.

Tot plegat, el que hem de comptar és quants nombres son de la forma $5aa5$, on $a$ és una xifra qualsevol entre $0$ i $9$. Llavors, és clar que hi ha exactament $\boxed{10}$ tals nombres.

Problema 6
4 punts   •   3 min

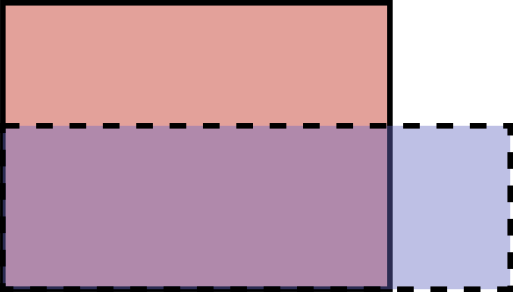
Un rectangle té una àrea de $48$ unitats quadrades. Si augmentem un costat en $2$ unitats i reduïm l’altre en $2$ unitats, l’àrea no canvia.

Quina és la mida del costat petit del rectangle inicial?

A. $7$
B. $\sqrt{19}$
C. $4$
D. $3\sqrt{5}$
E. $6$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 7
4 punts   •   3 min

Dues ciclistes, l’Anna i la Marta, estan separades per $60$ km. Comencen a pedalar l’una cap a l’altra al mateix temps. L’Anna va a $12$ km/h i la Marta va a $18$ km/h. Quants quilòmetres haurà recorregut la Marta quan es trobin?

A. $36$
B. $24$
C. $48$
D. $30$
E. $52$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 8
4 punts   •   3 min

En una fila hi ha $7$ cadires numerades de l’$1$ al $7$. La professora vol asseure-hi dos alumnes per a que facin un examen, però vol que els alumnes no ocupin cadires consecutives. De quantes maneres diferents és possible triar les cadires?

A. $42$
B. $20$
C. $21$
D. $15$
E. $7$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 9
4 punts   •   3 min

Tenim un cub gran de fusta de $3\times 3 \times 3$ cm pintat de blau només per fora. Si el tallem en petits cubs d'$1 \times 1 \times 1$ cm, quants d'aquests petits cubs tindran exactament dues cares pintades de blau?

A. $8$
B. $12$
C. $10$
D. Cap
E. $6$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 10
4 punts   •   3 min

A la pissarra escrivim tots els nombres naturals de l’$1$ al $50$ i n'esborrem els que són múltiples de $2$ o de $5$.

Quants nombres hi queden?

A. $25$
B. $20$
C. $30$
D. $15$
E. $18$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 11
5 punts   •   4 min 30 s

La Sara té dues goteres a casa seva. Una goteja exactament cada $6$ segons i l'altra exactament cada $14$. Si just acaben de caure dues gotes alhora de cadascuna, quantes vegades tornarà a passar en els propers $5$ minuts? (sense comptar aquesta vegada).

A. $3$
B. $7$
C. $5$
D. $4$
E. $6$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 12
5 punts   •   4 min 30 s

Quin nombre és més gran: $2^{100}$, $3^{75}$, $4^{50}$ o $5^{25}$?

A. $2^{100}$
B. $3^{75}$
C. $4^{50}$
D. $5^{25}$
E. Són tots iguals
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 13
5 punts   •   4 min 30 s

En un torneig d'escacs ràpids, cada participant juga exactament una partida contra tots els altres. Si en total s'han jugat $45$ partides, quants participants hi ha?

A. $23$
B. $44$
C. $10$
D. $5$
E. $9$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 14
5 punts   •   4 min 30 s

En un triangle isòsceles, els costats iguals mesuren $5$ i l’altre $6$. Quina és l’àrea del triangle?

A. $12$
B. $6$
C. $8$
D. $10\sqrt{2}$
E. $4\sqrt{3}$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 15
5 punts   •   4 min 30 s

Cinc alumnes estan intentant recordar quin dia van fer l’examen de matemàtiques, perquè el professor està trigant massa en corregir i volen presentar una queixa a la cap d’estudis.

  • L'Aniol diu: «L’examen va ser dilluns.»
  • El Bru diu: «L’examen va ser més a prop del dilluns que del divendres.»
  • La Carla diu: «L’examen va ser passat el dilluns.»
  • La Duna diu: «L’examen va ser abans del dimecres.»
  • L'Èlia diu: «L’examen no va ser dilluns.»

Si exactament una persona s’equivoca, quin dia va ser l’examen?

A. Dilluns
B. Dimarts
C. Dimecres
D. Dijous
E. Divendres
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Concurs 2n d'ESO
Estudiants que cursen 2n d'ESO o un curs inferior.

# Usuari Punts Respostes
1. 2n d'ESO  Jansan 91
2. 2n d'ESO  MarcelM 90
3. 2n d'ESO  AleixK 89
4. 1r d'ESO  cesc_28 88
5. 1r d'ESO  elbruixot 86
6. 2n d'ESO  Milena_Arsenyan 85,25
7. 2n d'ESO  cmoliina 84,5
8. 2n d'ESO  Antaviana 80,75
9. 1r d'ESO  Kalajary27 80
◌
10. 2n d'ESO  isaac 76,75
11. 2n d'ESO  Júlia_manez 76,5
12. 2n d'ESO  Marisol5@CR 76
13. 2n d'ESO  Miquel_M 75,25
14. 2n d'ESO  BRO 74,75
15. 1r d'ESO  Oleguer_Funosas 74,25
16. 1r d'ESO  InesHGF 73,75
17. 2n d'ESO  ElCangur 72,75
◌
17. 2n d'ESO  esther.alonso 72,75
◌
19. 1r d'ESO  Teo 72,25
20. 6è de Primària  PolSM 72
◌ ◌
21. 2n d'ESO  Maial 71,5
◌
21. 2n d'ESO  MarwaSemmane0 71,5
23. 2n d'ESO  Salvi 68
24. 2n d'ESO  Eilin_06 67,25
◌ ◌ ◌ ◌
25. 2n d'ESO  GuiuT 67
26. 2n d'ESO  AngieMaas 66
◌ ◌
27. 1r d'ESO  Elies 65,5
27. 2n d'ESO  Zihan_hoja 65,5
29. 1r d'ESO  Júlianavarro 64,75
30. 2n d'ESO  AAMdri 64
◌
◌
31. 1r d'ESO  AlmaJoveBuj 61,75
32. 1r d'ESO  JúliaG 59,5
33. 2n d'ESO  BlaiLT 57,75
◌
◌
◌
34. 6è de Primària  Pir2 57
35. 2n d'ESO  Mina 56,75
36. 2n d'ESO  Niko 54,5
37. 2n d'ESO  Núria.Romero.Vilas 53,5
◌
◌
38. 2n d'ESO  V1nwebs2 53,25
39. 6è de Primària  Origami2.0 50,5
40. 1r d'ESO  Janbars 45,75
41. 2n d'ESO  Elpro9 45
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌
42. 1r d'ESO  25amirelhaouariaddali 44
43. 4t de Primària  SonGoku 43,25
◌ ◌
44. 1r d'ESO  jordina1608 41
45. 2n d'ESO  AMA85 35
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌
46. 1r d'ESO  Z99 34,5
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌
47. 2n d'ESO  Asmaa-Laaraj-Zouba15 29,75
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌
48. 2n d'ESO  KRUKO 27,25
◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌

Concurs obert
Usuaris que han superat 2n d'ESO, professors, etc.

# Usuari Punts Respostes
1. 2n de Batxillerat  lluc.galindo 91
2. 4t d'ESO  Cristian_García 90
3. 1r de Batxillerat  OG_JAP 88
4. 2n de Batxillerat  MCuadros 85,25
5. 2n de Batxillerat  eva.pascual 83,25
6. 3r d'ESO  AleixBala 78,25
7. 3r d'ESO  Alfonsopg 70,25
8. Professor/a  Emas4 65,75
◌
9. Professor/a  Nurieta 65,25
◌
10. 3r d'ESO  NoahFadriqueAraque 49,75
◌ ◌ ◌ ◌
11. Professor/a  mon 37,25
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
12. Universitat  Oriol47 34
◌ ◌ ◌ ◌
◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌

Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.

# Usuari Punts Respostes
1. 3r d'ESO  Naia_Azañedo 100
1. 6è de Primària  Pir2 100
3. 1r d'ESO  Z99 98
4. Curs indeterminat  izancorral20 96
◌
4. 1r d'ESO  Sergiperelló@madina 96
6. 2n d'ESO  kevingallardo20 95
6. 1r d'ESO  rodrigobustosñoñi@madina 95
◌
8. 1r d'ESO  HanselCevallosadios@madina 92
9. 1r d'ESO  youssef 89
10. 2n d'ESO  lil_lassana 84,25
11. 1r d'ESO  lluciamoragues@madina 82,5
12. 2n d'ESO  khadijagul24 79,5
◌
13. 2n d'ESO  Aynitaaa12 79
14. 1r d'ESO  guillem_biosca 77,75
15. 1r d'ESO  pablocalongecano_10130@madina 73,75
◌ ◌
16. 2n d'ESO  Abrazada 73,5
◌
17. 2n d'ESO  iraatiib 72
18. 2n d'ESO  xanel 60,5
19. 1r d'ESO  IrayGallardo1C@madina 59,25
20. 2n d'ESO  Eduardo_Barruz 44
21. 1r d'ESO  Arnau.G.B. 27,75
◌
◌

Llegenda

  →   Resposta correcta

  →   Resposta correcta més ràpida de la taula (+1 punt)

  →   Resposta incorrecta