Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.
Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.
Problema 1
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Quines són les dues últimes xifres del nombre $5^{2026}$?
Mirem les primeres potències de $5$
$$ 5^1 = 5, \qquad 5^2 = 25, \qquad 5^3 = 125, \qquad 5^4 = 625, … $$ i veiem que a partir de la segona potència, tots semblen acabar en $25$. Efectivament això és cert, i anem a demostrar-ho més formalment per inducció.
Tenim el cas base $5^2 = 25$, que acaba en $25$. De fet, hem comprovat també que es compleix pels següents casos, però amb un sol cas base és suficient.
Ara, suposem que tenim $n > 2$ un enter, i que per tots els enters anteriors $k$ compresos entre $2$ i $n-1$ es compleix que $5^k$ acaba en $25$.
Aleshores, escrivim $5^n = 5 \cdot 5^{n-1}$, i podem usar la hipòtesi d’inducció: tenim que $5^{n-1} = 100 a + 25$ per a algun enter $a$, ja que les últimes dues xifres son $25$. Llavors
$$ 5^n = 5 \cdot (100 a + 25) = 100 \cdot (5 \cdot a) + 125 = 100 \cdot (5 \cdot a + 1) + 25 $$
Així que l’afirmació és certa també per a $n$. Això prova el pas inductiu, i tot plegat que demostrat, pel principi d’inducció matemàtica, que totes les potències de $5$ a partir de la segona acaben en $\boxed{25}$.
Problema 2
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Quants triangles podem trobar dibuixats en la següent figura, sense afegir cap segment?
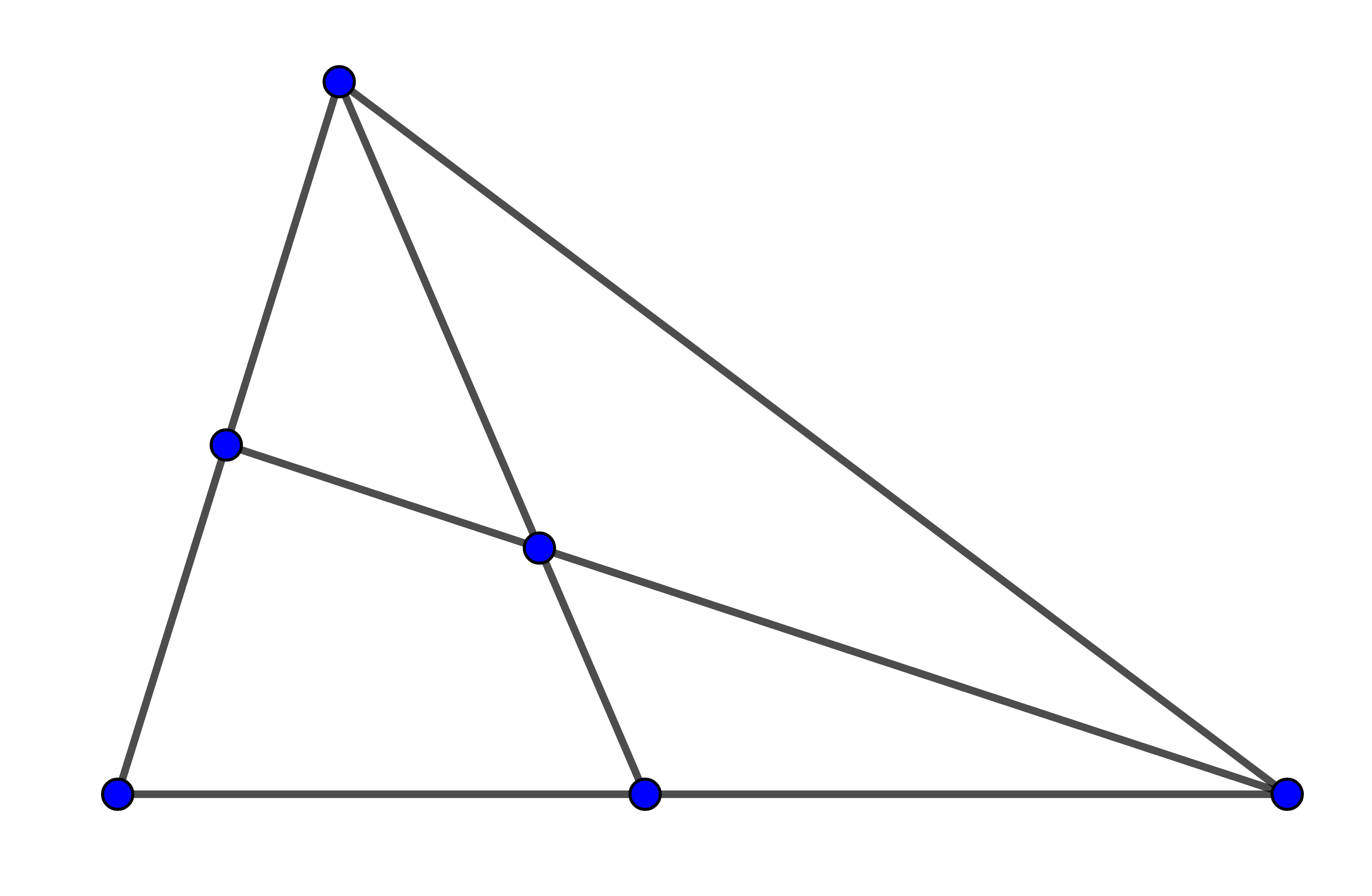
Nota: Per exemple, tenim
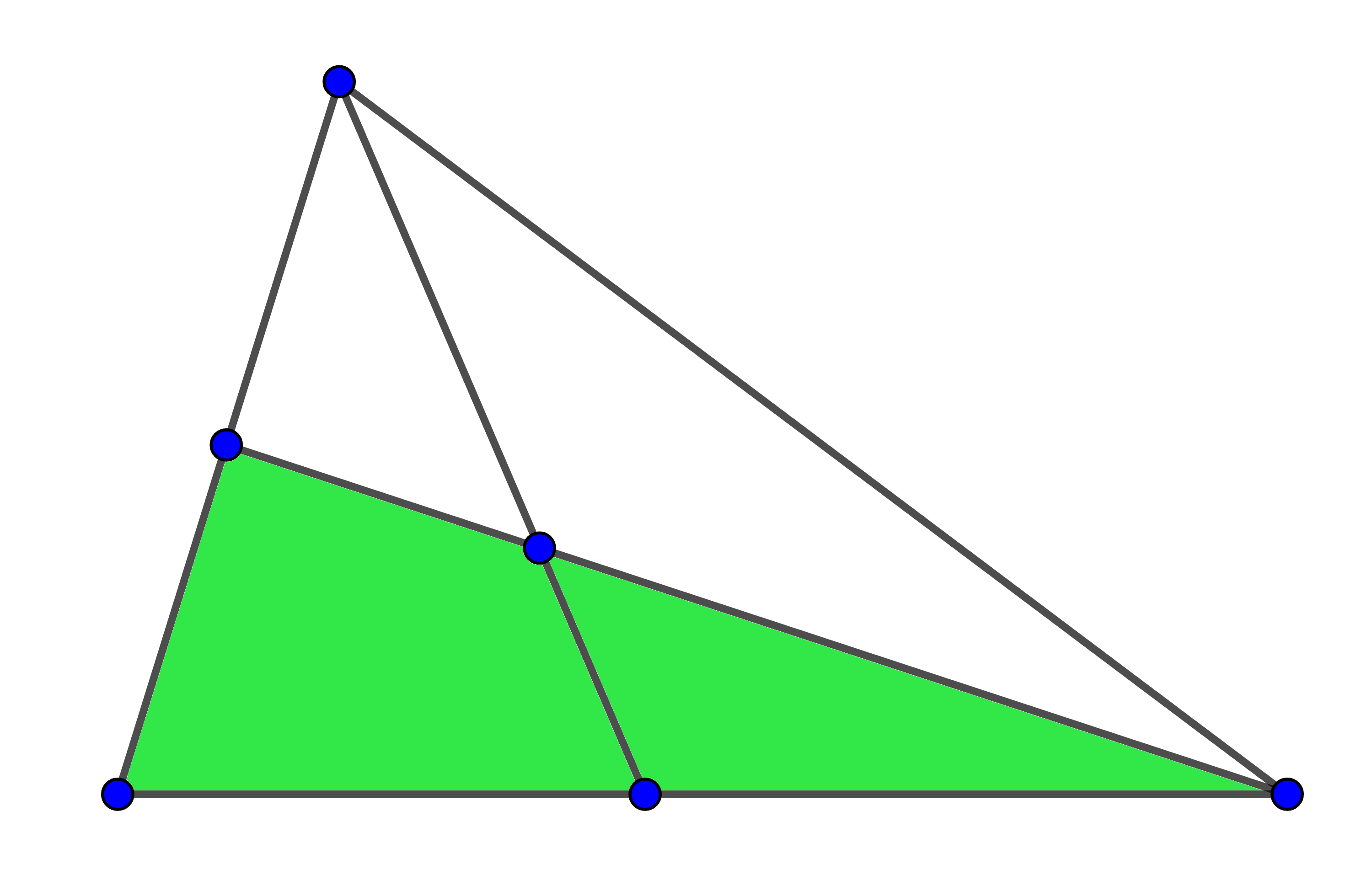
Vegem que podem trobar-hi $8$ triangles. Per a comptar-los, anem a distingir segons el nombre de regions.
Usant només una de les regions que hi ha a la figura, tenim $3$ possibilitats:
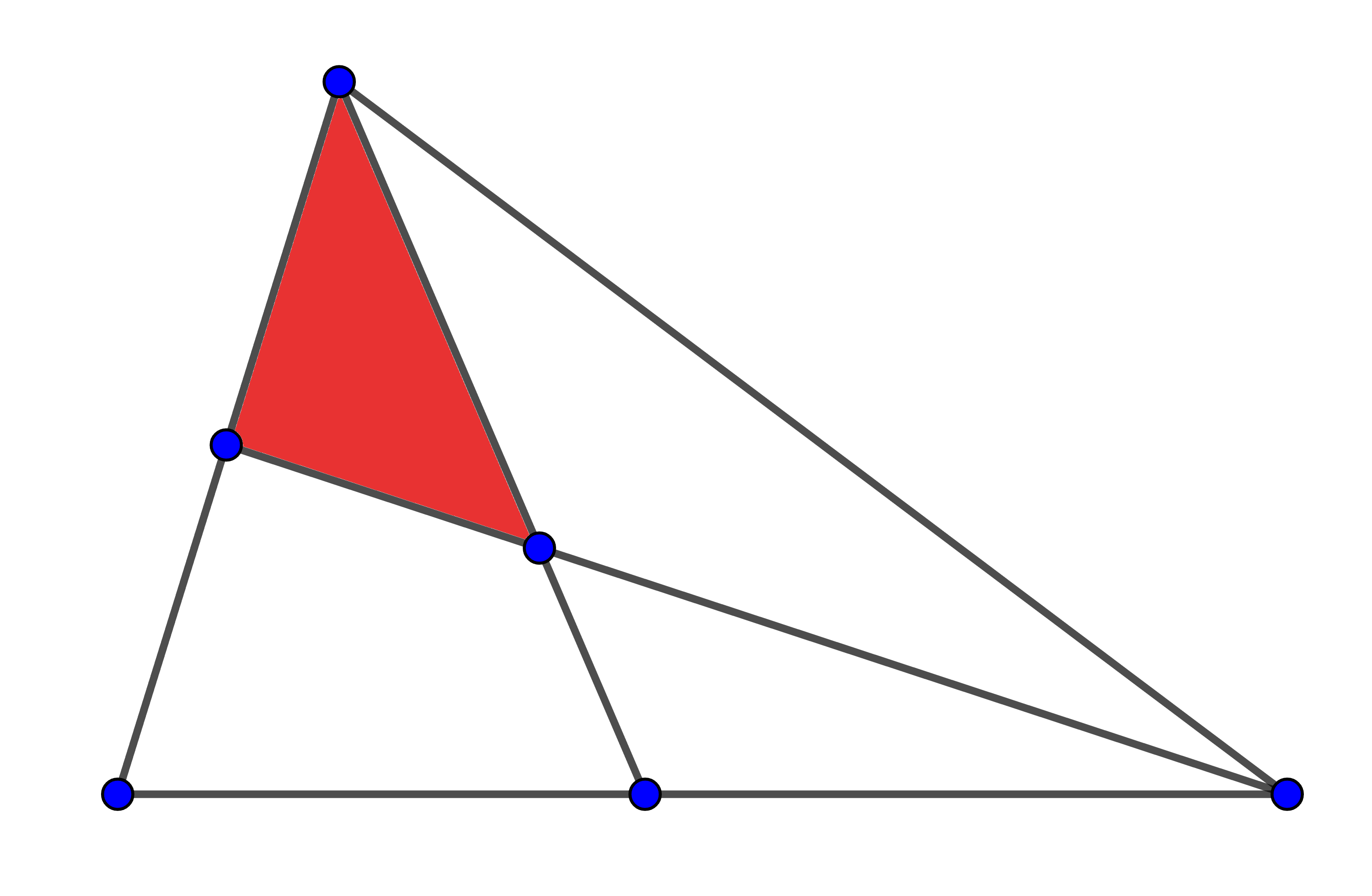
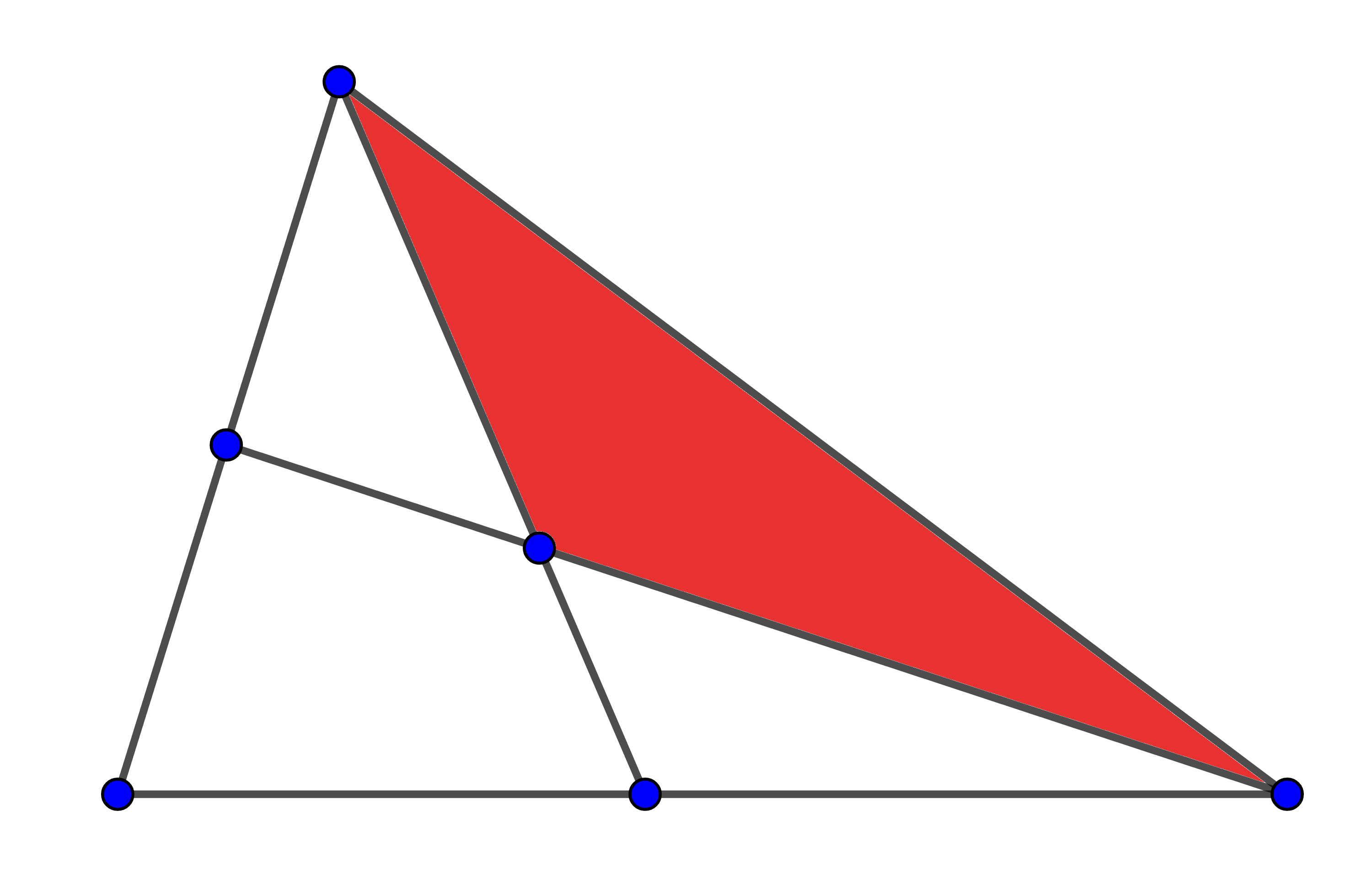
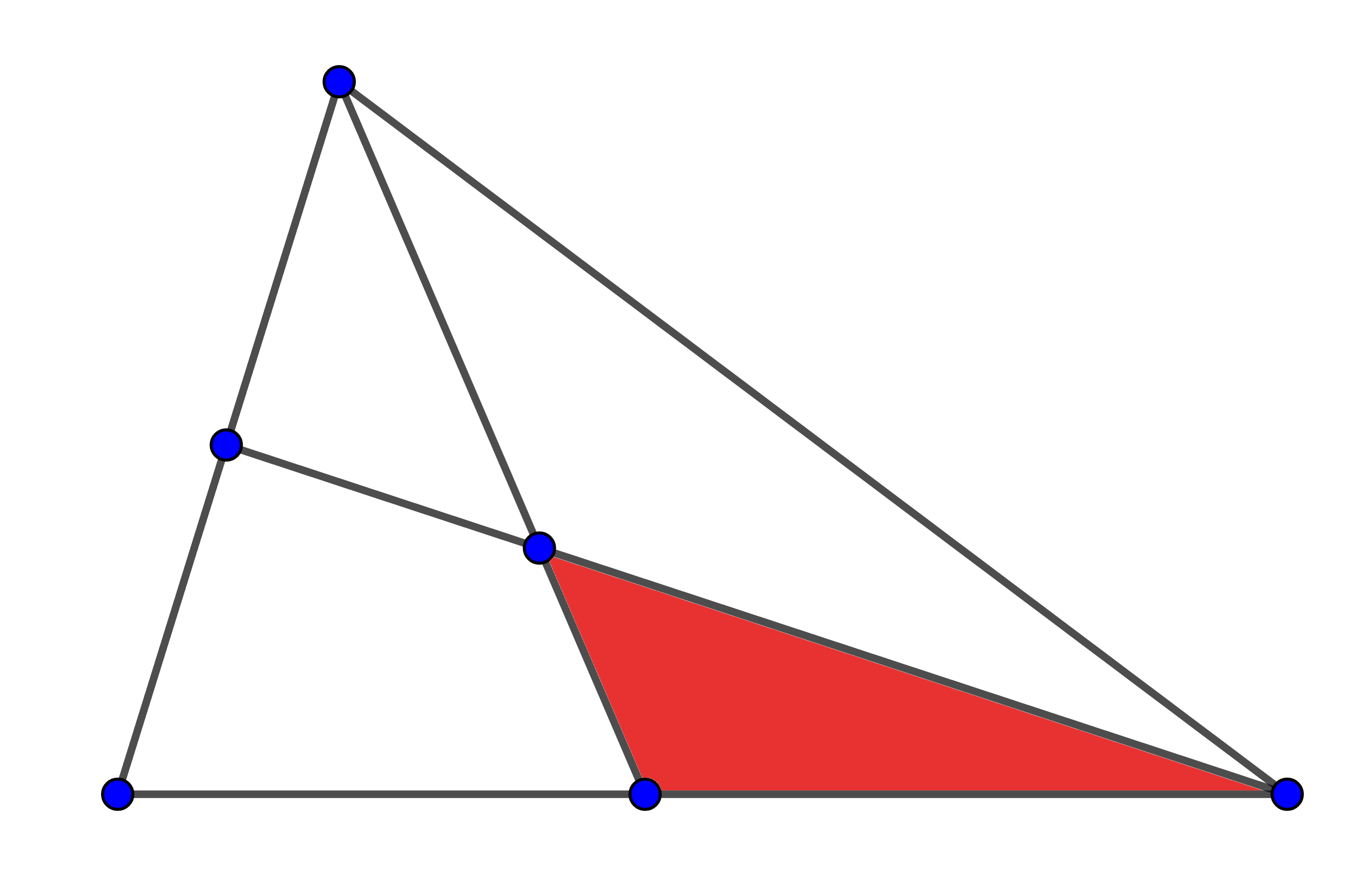
Usant excatament dues de les regions que hi ha a la figura, tenim $3$ possibilitats:
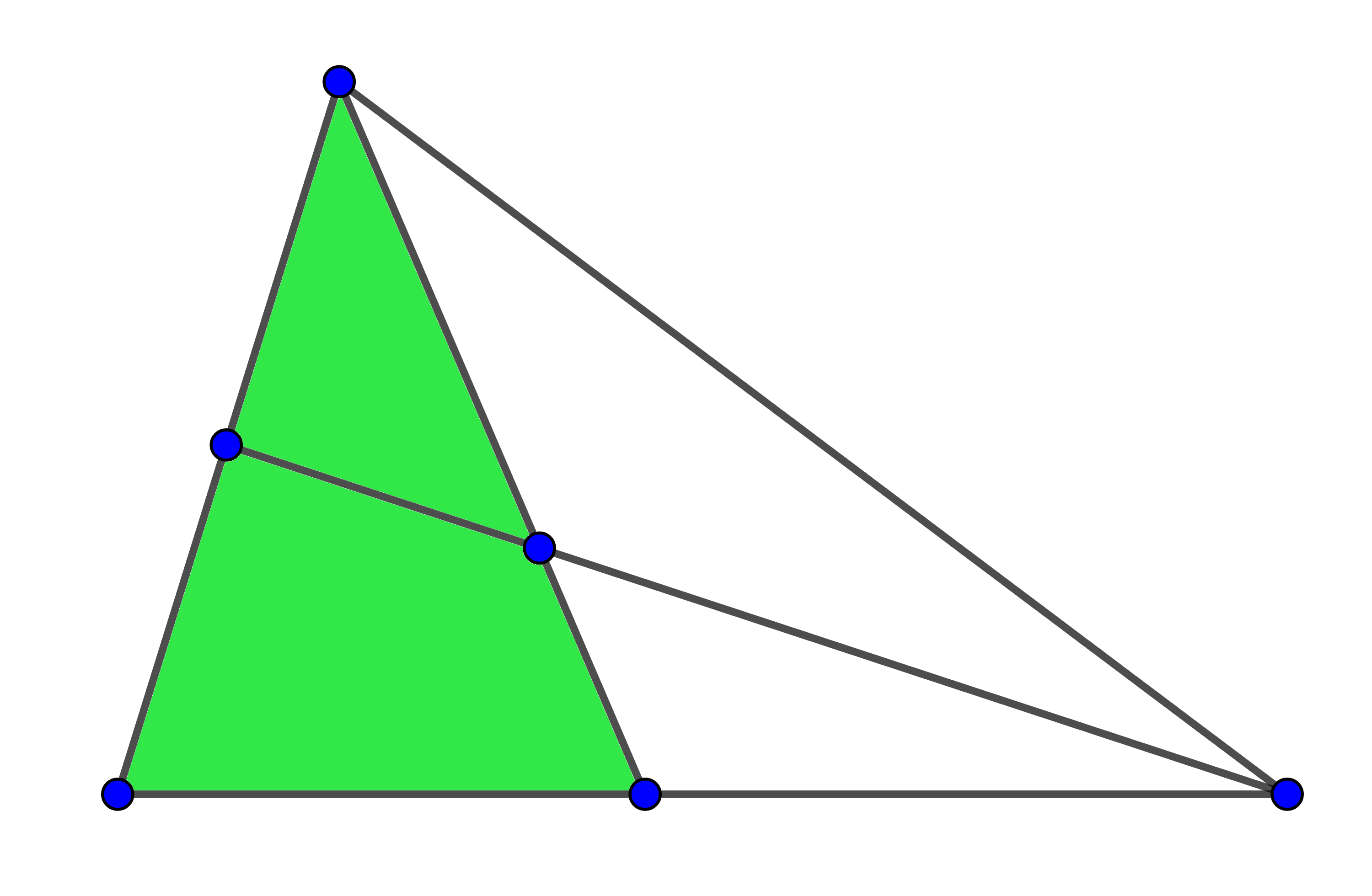

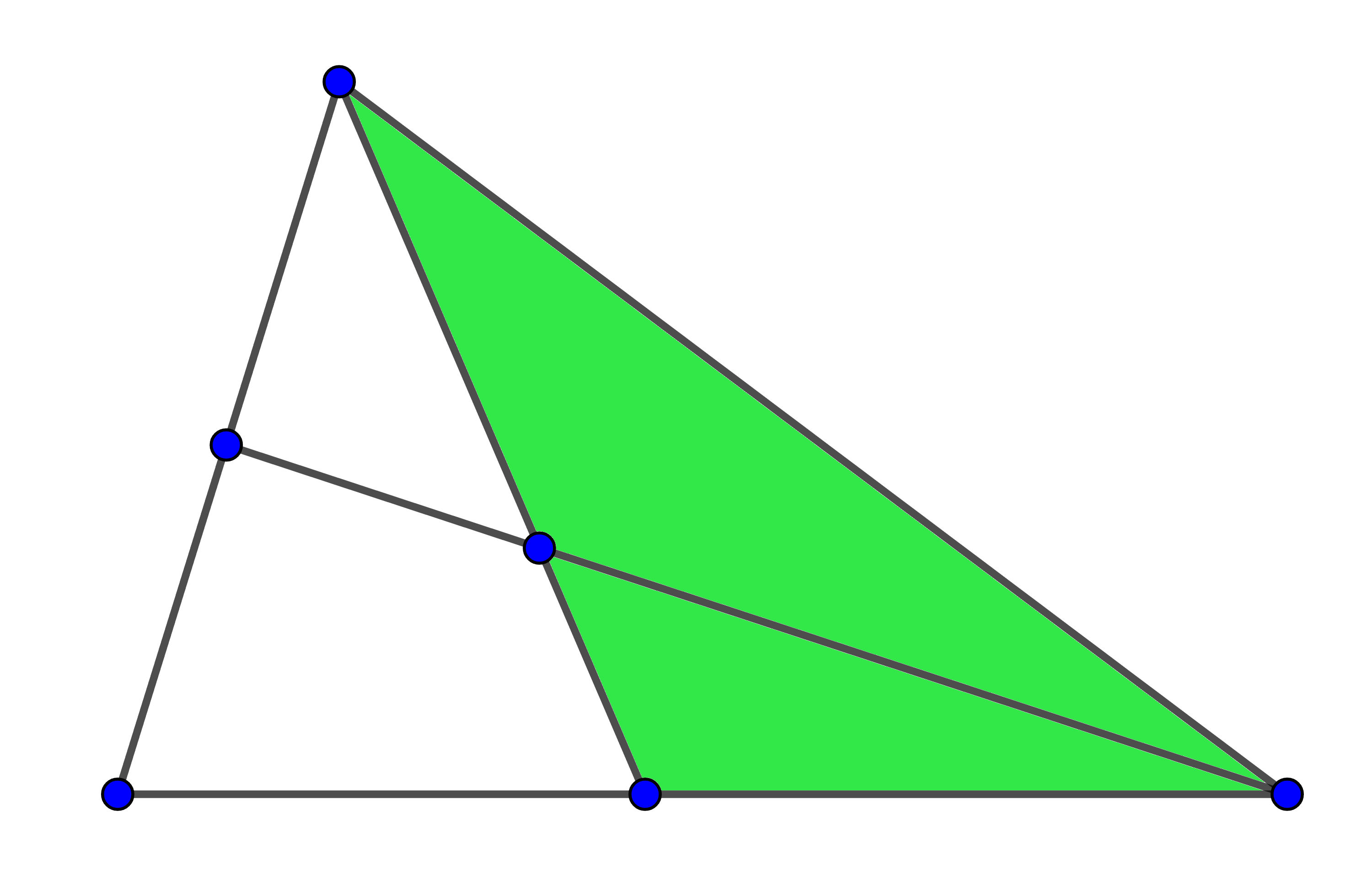
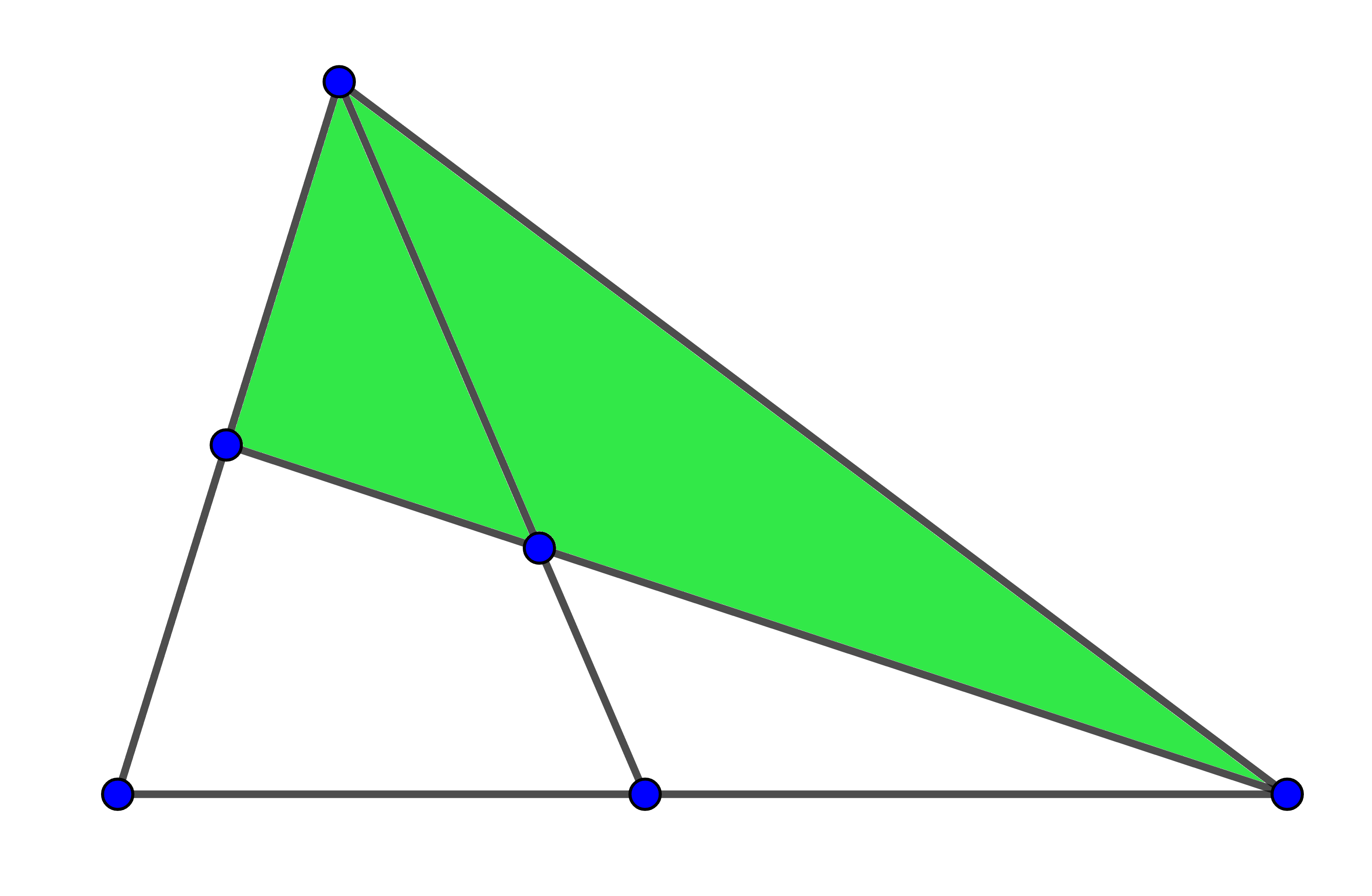
Usant exactament tres regions, podem provar que és impossible formar un triangle.
Finalment, usant totes les regions podem formar un únic triangle:
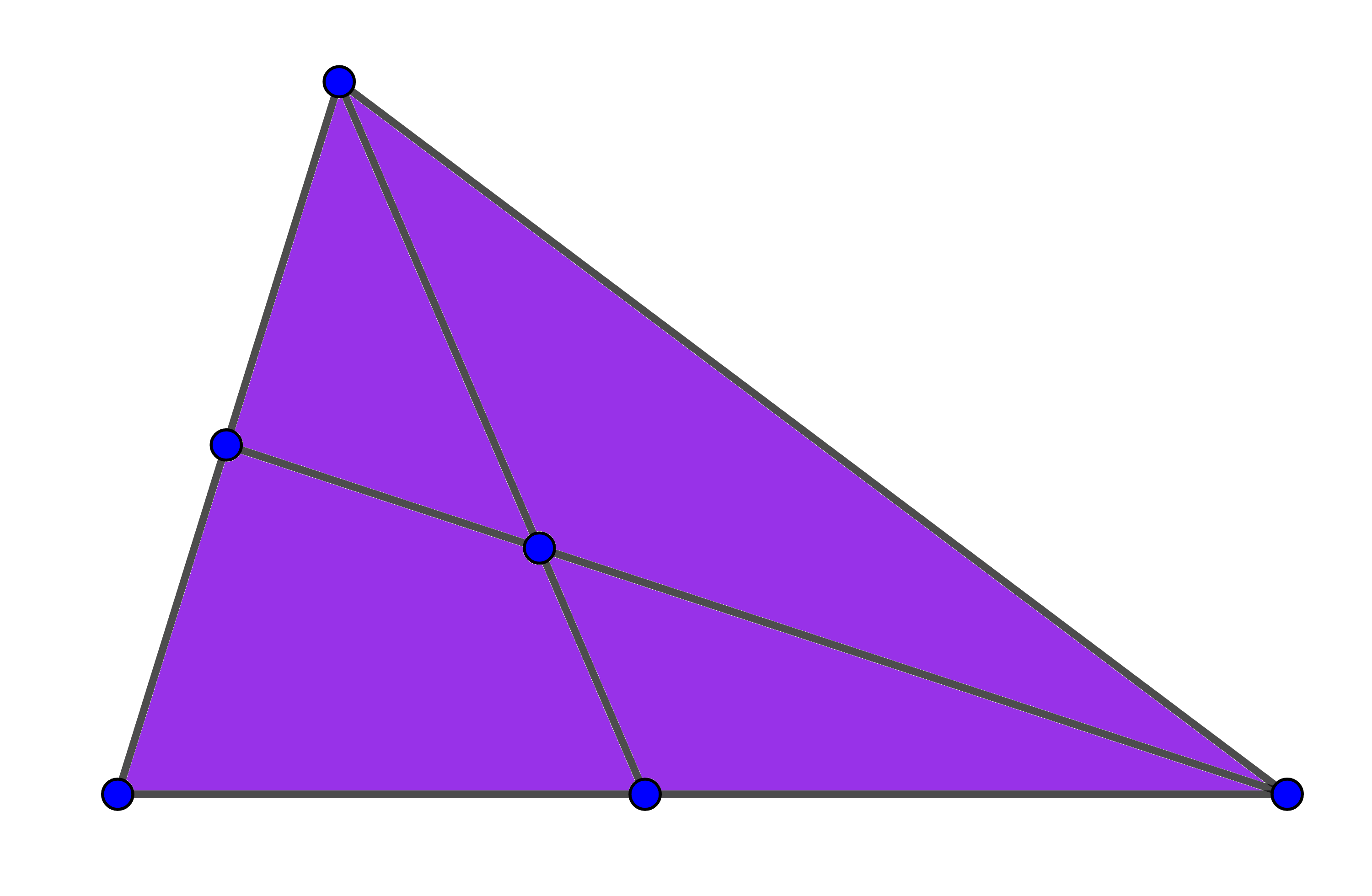
Per tant, tot plegat, la respota cercada és $3+4+1=\boxed{8}$.
Problema 3
3 punts
1 min
30 s
3 punts
•
1 min
30 s
Diem que un nombre és ric si té totes les seves xifres diferents, i diem que un nombre és pessimista si les seves xifres (d'esquerra a dreta) estan en ordre decreixent.
Quants nombres de dues xifres són rics i pessimistes alhora?
Un nombre de dues xifres en ordre decreixent queda completament determinat per la tria de dues xifres diferents: la més gran ocuparà la posició de les desenes i la més petita, la de les unitats.
Partim del conjunt de les deu xifres possibles: $\{0,1,2,3,4,5,6,7,8,9\}$, i triem dues xifres diferents d’aquí. El nombre de maneres de fer-ho és el nombre combinatori
$$ {10 \choose 2} = \frac{10 \cdot 9}{2} = 45. $$
En efecte, tenim $10$ tries per a la primera xifra, i només $9$ per a la segona, ja que no podem repetir. Ara bé, cometríem un error en comptar el nombre de tries com $10 \cdot 9$, ja que, per exemple, és el mateix triar primer el $8$ i després el $6$, que a l’inrevés. Com que l’ordre en què les hem triat és indiferent, hem de dividir el producte anterior per $2$, i d’aquí el resultat.
Aleshores, per a cada parella de xifres triada, existeix exactament un nombre de dues xifres amb les xifres diferents i en ordre decreixent, col·locant la xifra més gran a les desenes i la més petita a les unitats. A més, tots els nombres amb aquesta propietat s’obtenen d’aquesta manera.
Per tant, el nombre de nombres de dues xifres amb xifres diferents i en ordre decreixent és $ \boxed{45}$ .
Problema 4
3 punts
1 min
30 s
3 punts
•
1 min
30 s
En un examen, la mitjana de les notes de $9$ alumnes és un $6$. Si arriba un desè alumne i la mitjana puja a un $6.3$, quina nota ha tret aquest últim alumne?
El punt important d’aquest problema és que no requerim saber les notes individuals de cada alumne, sinó la seva suma.
Inicialment, amb els primers nou alumnes, la suma total de notes serà $9 \cdot 6 = 54$, per definició de la mitjana.
Aleshores, amb el desè alumne, la suma de notes serà $10 \cdot 6.3 = 63$. Per tant, de la diferència entre aquestes dues quantitats podem deduir que la nota del desè alumne és
$$ 63 - 54 = \boxed{9} $$
Problema 5
3 punts
1 min
30 s
3 punts
•
1 min
30 s
El Víctor està intentant decidir un codi nou per al seu candau, que té $3$ xifres. Vol que el codi tingui dues xifres iguals, i l’altra diferent d'aquestes. De quantes maneres pot fer-ho?
Nota: Per exemple, codis vàlids per al Víctor serien: $112$, $343$…
Primer de tot, notem que tenim $3$ opcions per triar quina serà la posició que contingui la xifra diferent de les altres.
Segon, per a la posició que hem triat que contindrà la xifra diferent, tenim $10$ opcions per triar quina xifra tindrà.
Per últim, ens queda triar quina serà la xifra repetida, que ja sabem que ocuparà les dues altres posicions del codi. Com que han de ser diferents a la primera xifra escollida, només ens queden $9$ opcions.
Tot plegat, multiplicant obtenim el nombre de maneres totals: $3 \cdot 10 \cdot 9 = \boxed{270} $.
Problema 6
4 punts
3 min
4 punts
•
3 min
En una successió de nombres, cada terme (a partir del tercer) és la suma dels dos anteriors. Si el primer terme és $1$ i el quart és $11$, quin és el sisè terme?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 7
4 punts
3 min
4 punts
•
3 min
En un hexàgon regular, quantes maneres hi ha de triar $3$ vèrtexs que formin un triangle no isòsceles?
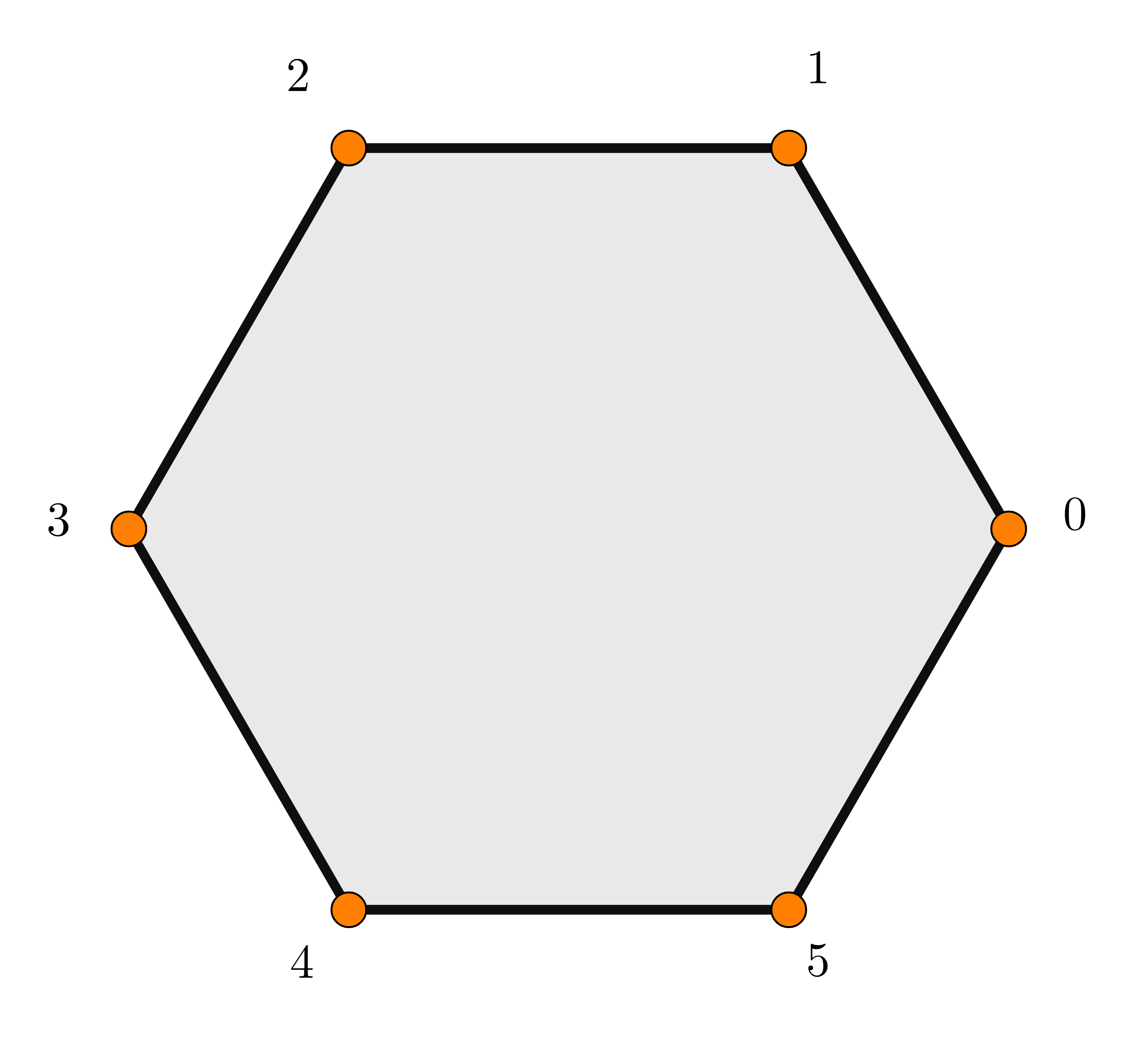
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 8
4 punts
3 min
4 punts
•
3 min
La suma de les edats d’un pare i el seu fill és $44$. D’aquí a dos anys, el pare tindrà el triple de l’edat del fill.
Quina edat té el pare actualment?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 9
4 punts
3 min
4 punts
•
3 min
De quantes maneres podem triar tres nombres diferents d’entre $\{2023, 2024, 2025, 2026, 2027, 2028\}$ perquè la seva suma sigui parella?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 10
4 punts
3 min
4 punts
•
3 min
Un cub de costat $4$ té una formiga situada en un vèrtex. La formiga camina sempre sobre les cares del cub (no pot travessar l’interior). Si vol arribar al vèrtex oposat del cub (el més llunyà possible de l’inicial), quina és la distància mínima que ha de recórrer?

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 11
5 punts
4 min
30 s
5 punts
•
4 min
30 s
En un torneig de pàdel per eliminatòries amb $64$ parelles, quants partits s’han de jugar per decidir la parella guanyadora?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 12
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Tenim dues espelmes de la mateixa longitud. Una tarda $4$ hores a consumir-se i l'altra $3$ hores. Si les encenem alhora, quant de temps passarà fins que una sigui el doble de llarga que l'altra?
Nota: Assumeix que les espelmes es consumeixen de forma lineal i uniforme.
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 13
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Un triangle té costats de longituds $5$, $12$ i $13$. Quina és la seva àrea?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 14
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Cinc amics estan fent una cursa i, en acabar tots, diuen el següent.
- Arnau: «La Berta ha arribat abans que jo.»
- Berta: «El Carles ha arribat després que jo.»
- Carles: «L’Arnau ha arribat abans que jo.»
- Dídac: «La Berta ha arribat després que el Carles.»
- Etna: «L’Arnau ha arribat després que el Carles.»
Sabem que exactament dos d’ells menteixen. En quin ordre poden haver arribat l’Arnau, la Berta i el Carles?
Nota: Per exemple, la resposta "Arnau, Berta, Carles" voldria dir que l'Arnau ha arribat abans que la Berta, i que la Berta ha arribat abans que el Carles.
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Problema 15
5 punts
4 min
30 s
5 punts
•
4 min
30 s
Una escala de $5$ m de llargada està recolzada en una paret vertical. Inicialment, la base de l'escala està a $3$ m de la paret. Si la part superior de l'escala llisca $1$ m cap avall, quants metres s'haurà desplaçat la base cap enfora?
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.
Concurs 4t d'ESO
Estudiants que cursen 4t d'ESO o un curs inferior.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | MarcelM | 88,25 |
|
| 2. | DavidSun | 85 |
◌
|
| 3. | Cristian_García | 84 |
◌
|
| 4. | Jaume_ | 82,25 |
|
| 5. | Starpot | 82 |
|
| 6. | Leyre | 79,25 |
|
| 7. | Alfonsopg | 77 |
|
| 7. | Milena_Arsenyan | 77 |
|
| 9. | jaulora | 75,5 |
|
| 10. | RogerC | 72,25 |
|
| 11. | NereaT | 72 |
|
| 12. | ainnn_tr | 71 |
|
| 13. | Montse2011 | 69,5 |
|
| 14. | Antaviana | 68,5 |
◌
|
| 14. | Jansan | 68,5 |
◌
|
| 16. | 073GrahamRayoChess | 68 |
|
| 16. | PauMartínezSánchez | 68 |
|
| 18. | TS | 67 |
◌
|
| 19. | Berta | 66,25 |
◌
|
| 20. | Hypergg2000 | 64,25 |
|
| 21. | Pir2 | 62,25 |
|
| 22. | gabibvv | 59,5 |
◌
|
| 23. | GB_010 | 59 |
|
| 24. | DidicG | 58,25 |
|
| 25. | Enric2010 | 57,25 |
|
| 26. | isaac | 52 |
◌
◌
◌
|
| 27. | Albasp | 49 |
◌
◌
|
| 28. | Origami2.0 | 47,75 |
|
| 29. | CRA | 47,25 |
|
| 30. | Lluc-ribas | 38 |
◌
|
| 31. | Eloi | 28,25 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
| 32. | SonGoku | 23,25 |
◌
|
Concurs obert
Usuaris que han superat 4t d'ESO, professors, etc.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | OG_JAP | 89,25 |
|
| 2. | lluc.galindo | 84,25 |
|
| 3. | eva.pascual | 82,25 |
|
| 4. | Frogrammer | 81,75 |
|
| 5. | Carbassa | 69,25 |
|
| 6. | Inma | 66,25 |
◌
|
| 7. | Nurieta | 55,25 |
|
| 8. | OGWHH | 29,75 |
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
◌
|
Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.
| # | Usuari | Punts | Respostes |
|---|---|---|---|
| 1. | LaiaMireia_18 | 99 |
|
| 2. | Naia_Azañedo | 74 |
◌
|
Llegenda
→ Resposta correcta
→ Resposta correcta més ràpida de la taula (+1 punt)
→ Resposta incorrecta


