Contrarellotge temàtica: el Sol (4t d'ESO)
Dimecres, 8 de març de 2017 a les 19:00

Enhorabona a tots els participants!

I especialment als guanyadors de la prova oficial: Julian, Arisb i MasterPlus.

Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.

Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Problema 1
3 punts   •   1 min 30 s

Pintem les cares exteriors d'un cub de $6\times6\times6$ format per petits cubs de $1\times1\times1$. Quants cubs petits s'han quedat sense pintar?
A. $125$
B. $152$
C. $64$
D. $61$
E. $98$
En blanc
Mostra solució
S'han quedat sense pintar tots els cubs que no hi són a la superfície. Això és el cub de $4\times4\times4$ de l'interior, en total: $$N_{\text{cubs petits}}=4^3=64$$

Problema 2
3 punts   •   1 min 30 s

Enguany ens ha deixat Raymond Smullyan, matemàtic americà autor de molts llibres de matemàtica recreativa. Vegem un dels deus problemes:

Un comerciant compra un ocell per $7$€, i el ven poc després per $8$€. El torna a comprar més endavant per $9$€ i l'acaba venent per $10$€. Quin benefici ha obtingut?

A. Cap: es queda igual
B. Cap: perd $1$€
C. $1$€
D. $2$€
E. Cap de les anteriors
En blanc
Mostra solució
En total s'ha gastat $7+9=16$€, i n'ha ingressat $8+10=18$€, per tant ha guanyat $18-16=2$€. Adonem-nos que tant se val si el segon ocell que comprat és el mateix que l'inicial o un altre.

Problema 3
3 punts   •   1 min 30 s

Si $x$ és un número enter negatiu, quina expressió serà sempre la més gran?
A. $x+1$
B. $2x$
C. $-2x$
D. $6x+2$
E. $x-2$
En blanc
Mostra solució

Si prenem per el $-1$ i avaluem, tenim que:

  • $x+1 = -1 + 1 = 0$
  • $2x = 2\cdot(-1) = -2$
  • $-2x = -2\cdot(-1) = 2$
  • $6x+2 = 6\cdot(-1)+2 = 0$
  • $x-2=-1-2=-3$
És fàcil observar que a mesura que $x$ disminueix, l'expressió $-2x$ és la única que augmenta de valor.

Problema 4
3 punts   •   1 min 30 s

Quin número hi ha exactament enmig de $\frac12$ i $\frac43$?
A. $\frac{3}{4}$
B. $\frac{5}{6}$
C. $\frac{5}{8}$
D. $\frac{7}{8}$
E. $\frac{11}{12}$
En blanc
Mostra solució
Fem la mitjana: $$\frac{\frac12 + \frac43}2=\frac{\frac{11}6}{2}=\frac{11}{12}$$

Problema 5
3 punts   •   1 min 30 s

Amb quants zeros acaba el producte dels primers $100$ nombres primers?
A. $0$
B. $1$
C. $2$
D. $100$
E. $1000$
En blanc
Mostra solució

Per acabar amb $0$ un número, ha de ser múltiple de $10$. Si acaba amb $2$ zeros serà múltiple de $10^2=100$, etc.

Entre els primers $100$ nombres primers només apareix un cop el factor $2$ i un cop el factor $5$, de manera que el producte de tots els números serà múltiple de $10$, però no de $100$. Per tant, acaba amb $1$ zero.

Problema 6
4 punts   •   3 min

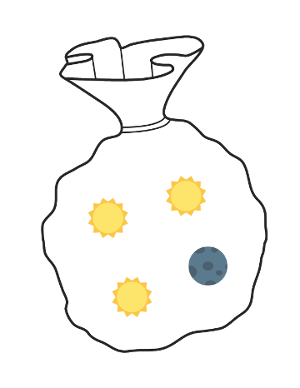
A una bossa tenim $3$ sols i $1$ lluna. Si sense mirar en traiem tres aleatòriament, quina és la probabilitat de triar els $3$ sols?

A. $\frac25$
B. $\frac12$
C. $\frac13$
D. $\frac14$
E. $\frac16$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 7
4 punts   •   3 min

EL 28 d'abril de 1930 va haver un eclipsi solar. Si el proper eclipsi va ser $176$ dies després, quin dia del mes va ocórrer aquest segon eclipsi? (Si el proper hagués sigut a l'endemà, diríem que va ser $1$ dia després).
A. $18$
B. $19$
C. $20$
D. $21$
E. $22$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 8
4 punts   •   3 min

A cadascuna de les $7$ figures del Tetris:

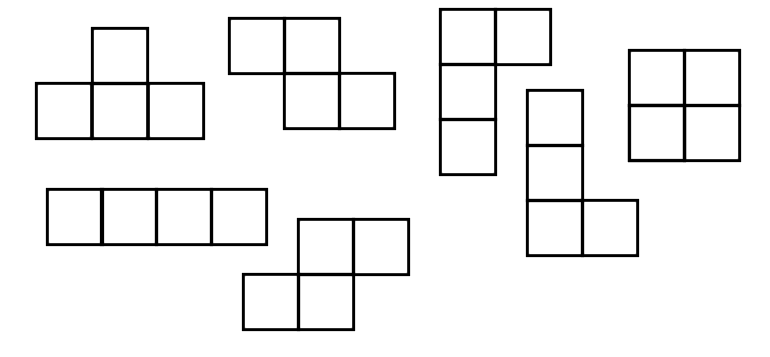
Li afegim un quadrat on vulguem, sempre que tinga un costat coincident amb el costat d'algun dels quadrats de la figura. Per exemple:

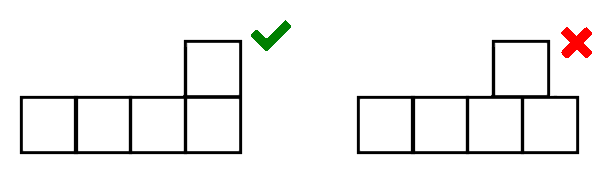
Quin és el màxim nombre de les figures resultants que tinguin algun eix de simetria?

A. $3$
B. $4$
C. $5$
D. $6$
E. $7$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 9
4 punts   •   3 min

Avui, 8 de març, és el dia internacional de les dones. Per fer el símbol de la dona, retallem una creu quadrada (tots els costats mesuren $1$) a l'interior d'una cartolina rodona morada, com veiem a la figura:

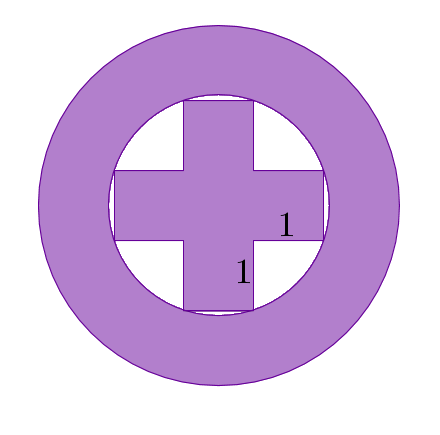
Quina és l'àrea de la zona que rebutgem (en blanc)?

A. $\frac52\pi-5$
B. $3\pi-5$
C. $10\pi-5$
D. $2\pi$
E. $\frac72\pi-5$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 10
4 punts   •   3 min

Alba, Balma i Carla ens proposen una endevinalla. Cadascuna d'elles ha decidit mentir o dir la veritat, i sempre ho compleixen. Ens diuen:

— Alba diu: Balma menteix!

— Balma diu: Carla menteix!

— Carla diu: Alba i Balma menteixen!

Qui diu la veritat?

A. Alba
B. Balma
C. Carla
D. Alba i Balma
E. Totes menteixen
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 11
5 punts   •   4 min 30 s

Situem $5$ punts $P_1,\,P_2,\,\ldots,\,P_5$ sobre una recta:

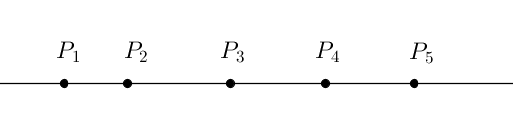
Triem un altre punt $Q$ de la recta i calculem la suma de les distàncies de $Q$ a cadascun dels altres punts.

On hem de situar $Q$ per tal de minimitzar aquesta suma?

A. $\frac{P_1+P_5}2$
B. $\frac{P_2+P_4}2$
C. $P_2$
D. $P_3$
E. Depén dels punts
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 12
5 punts   •   4 min 30 s

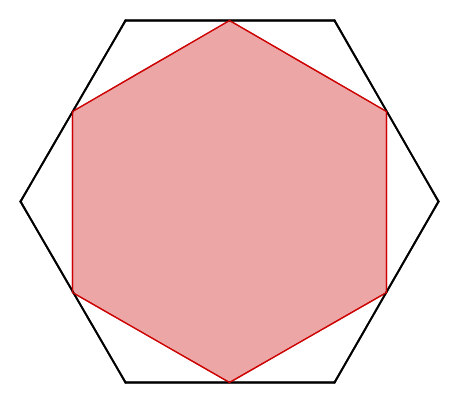Unint els punts mitjos dels costats d'un hexàgon regular, construïm un altre hexàgon regular més petit (vermell): Quina proporció de l'hexàgon gran està ocupada per l'hexàgon interior vermell?
A. $\frac12$
B. $\frac23$
C. $\frac34$
D. $\frac45$
E. $\frac\pi4$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 13
5 punts   •   4 min 30 s

Un enter $n$ té exactament $2$ divisors. $n+1$ en té exactament $3$. Quants divisors té $n+2$?
A. 2
B. 3
C. 4
D. Depén de $n$
E. Cap $n$ ho compleix
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 14
5 punts   •   4 min 30 s

Donat un triangle rectangle, dibuixem un quadrat amb dos costats sobre els catets i un vèrtex sobre la hipotenusa:

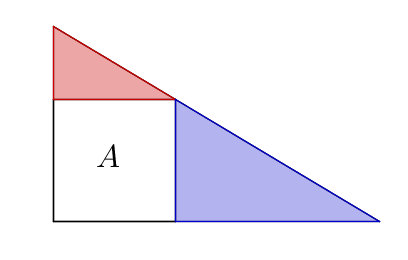
Anomenem $A$ l'àrea del quadrat. Si l'àrea del triangle vermell és: $$A_{\text{vermell}}=m\cdot A$$ Quina és l'àrea del triangle blau?

A. $\frac{A}{2m}$
B. $\frac{A}{3m}$
C. $\frac{A}{4m}$
D. $\frac{m}{A}$
E. $\frac{A}{m+2}$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 15
5 punts   •   4 min 30 s

El Sol és una estrella activa que sovint produeix erupcions solars $(E)$ i explosions de gas $(G)$, les quals els astrònoms sempre vigilen perquè poden danyar els satèl·lits i els astronautes.

Certa setmana hi han hagut dues explosions de gas en dies diferents. Per altra banda, també hi han hagut dues erupcions solars en dies diferents (entre elles dues).

Quina és la probabilitat que almenys una erupció i una explosió hagin coincidit el mateix dia?

A. $\frac{23}{42}$
B. $\frac{4}{7}$
C. $\frac{3}{7}$
D. $\frac{10}{21}$
E. $\frac{11}{21}$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Concurs 4t d'ESO
Estudiants que cursen 4t d'ESO o un curs inferior.

# Usuari Punts Respostes
1. 3r d'ESO  469 73,75
◌
2. 4t d'ESO  Arisb 59,25
3. 3r d'ESO  MasterPlus 50,75
4. 1r de Batxillerat  Gauss 49,5
◌ ◌
◌
◌
5. 3r d'ESO  lauraconejero11 48,25
6. 4t d'ESO  Patricia 47
◌ ◌
7. 4t d'ESO  arnaupadres 46,5
◌
8. 3r d'ESO  andrea02 46,25
9. 4t d'ESO  CintaArnau 45,75
◌
10. 3r d'ESO  sergilopezlopez5 43
◌ ◌
11. 3r d'ESO  asantosn 42,25
11. 3r d'ESO  nerea 42,25
13. 4t d'ESO  martijuanola 42
◌
14. 3r d'ESO  Lledóestevez 41,25
15. 3r d'ESO  JorgeSerrano 40,75
15. 3r d'ESO  Ssr 40,75
◌
◌
◌ ◌ ◌
17. 3r d'ESO  FRANPASTOR 39,5
18. 4t d'ESO  alba_pitarch19 38
◌
◌
19. 3r d'ESO  BeaT 36,75
20. 4t d'ESO  ViviCan28 35
◌
◌
21. 3r d'ESO  ainhoaserra 33,5
21. 3r d'ESO  Cristina 33,5
23. 2n d'ESO  nayla_1108 33
24. 3r d'ESO  angela_clemente 32,25
25. 3r d'ESO  MarcGar55555 32
◌
25. 3r d'ESO  Paula 32
27. 3r d'ESO  pauulaa8 31,75
◌
28. 4t d'ESO  ainaazkv 30
◌
◌ ◌ ◌
◌ ◌ ◌
29. 3r d'ESO  Adrianmadueno 28,75
◌
◌
30. 3r d'ESO  manullobregat 28
◌
◌
31. 3r d'ESO  JPG 27,75
◌ ◌ ◌ ◌ ◌
◌ ◌
32. 3r d'ESO  albaem 27,5
◌
◌
33. 3r d'ESO  andreagazu 27,25
34. 3r d'ESO  carlosdo 26
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
35. 3r d'ESO  Diflon 21,75
◌
36. 4t d'ESO  eulaliap 20,5
◌
◌
37. 4t d'ESO  Miriam 18,5
◌ ◌
38. 3r d'ESO  Lorena 16,25
◌ ◌
◌
39. 4t d'ESO  Miquel 15,75
◌ ◌ ◌ ◌ ◌
◌ ◌
40. 4t d'ESO  marcmon 10,75
◌
41. 2n d'ESO  laiaruiz 10

Concurs obert
Usuaris que han superat 4t d'ESO, professors, etc.

# Usuari Punts Respostes
1. Universitat  pcartanya 87,75
2. Professor/a  PACOVES 66,25
◌
◌ ◌
3. 4t d'ESO  JuanGuijarro 35,5
◌ ◌ ◌ ◌
4. 3r d'ESO  andreacollazos 34,5
5. 3r d'ESO  pablopoker7 33
◌

Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.

# Usuari Punts Respostes
1. Universitat  nestor 96
2. Curs indeterminat  melyazidibb 77,25
3. Curs indeterminat  eli.arqu 58,75
4. Universitat  JoanFP 54,5
5. Universitat  hugo_pb 51,5
6. Universitat  rvivob 30,5
◌ ◌
◌ ◌ ◌
◌ ◌ ◌

Llegenda

  →   Resposta correcta

  →   Resposta correcta més ràpida de la taula (+1 punt)

  →   Resposta incorrecta