Contrarellotge temàtica: el temps (2n de Batxillerat)
Dilluns, 23 d’octubre de 2017 a les 19:00

Premi: Taller al Museu de Matemàtiques de Catalunya


El primer classificat a la Contrarellotge guanyarà un val per 4 persones per visitar el Museu de Matemàtiques de Catalunya i realitzar el taller de «Les cúpules de Leonardo».

Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.

Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Problema 1
3 punts   •   1 min 30 s

Cinc xocolatines valen $8$ euros més que una xocolatina. Quants euros val una xocolatina?
A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
En blanc
Mostra solució
Els $8$ euros de més es deuen a $4$ xocolatines. Per tant, cada xocolatina val $8\div4=2$ euros.

Problema 2
3 punts   •   1 min 30 s

El monstre d'un malson té $5$ braços, i cada cop que li'n talles un, li'n surten $5$ allà on abans hi era. Si li talles $6$ braços mentre t'hi baralles, quants braços té al final el monstre?
A. $25$
B. $28$
C. $29$
D. $30$
E. $35$
En blanc
Mostra solució
Per cada braç que tallem, n'afegim $5$; per tant, cada tall implica $4$ braços més per al monstre. Al final, en tindrà: $$N_\text{braços}=5+6\cdot4=29$$

Problema 3
3 punts   •   1 min 30 s

Un mes ha tingut $5$ dimecres. Aquest mes no pot haver tingut:
A. $5$ dijous
B. $5$ dimarts
C. $5$ dilluns
D. $5$ divendres
E. $5$ dissabtes
En blanc
Mostra solució

En $28$ dies, que són $4$ setmanes, hi ha $4$ dies de cada.

En $29$ dies, ja podríem tindre $5$ dimecres, que haurien de ser el primer i l'últim d'aquests $29$ dies. En total un mes pot tenir $31$ dies com a molt, per tant, podríem afegir un dimarts o un dilluns al principi dels $29$ dies, o un dijous i un divendres al final.

El que no podem fer en cap cas és tindre un mes amb $5$ dissabtes.

Problema 4
3 punts   •   1 min 30 s

Llancem dos daus. Quina és la probabilitat que la suma siga menor que $5$?
A. $\frac15$
B. $\frac14$
C. $\frac16$
D. $\frac5{36}$
E. $\frac13$
En blanc
Mostra solució
Dels $6\cdot6=36$ possibles resultats, hi ha $6$ que donen un suma menor que $5$: $$11,\;12,\;21,\;13,\;31,\;22$$ Per tant, la probabilitat és: $$P=\frac6{36}=\frac16$$

Problema 5
3 punts   •   1 min 30 s

Si $x < 0$, quina de les opcions representa un nombre positiu?
A. $\frac{x}{|x|}$
B. $-x^2$
C. $(-x)^{-1}$
D. $\sqrt[3]{x}$
E. $-x^{-4}$
En blanc
Mostra solució

Repassem cada opció:

  • $\frac{x}{|x|}$: el numerador és negatiu i el denominador positiu, per tant serà negatiu.
  • $-x^2$: $x^2$ serà positiu, i per tant el signe menys el convertirà en negatiu.
  • $(-x)^{-1}$ : un positiu elevat a $-1$ serà positiu. Aquesta és la solució, doncs.
  • $\sqrt[3]{x}$: l'arrel cúbica d'un nombre negatiu continuarà sent negativa.
  • $-x^{-4}$: $x^{-4}=\frac{1}{x^4}$, i com l'exponent és parell, el resultat serà positiu. El signe menys convertirà el nombre en negatiu.

Problema 6
4 punts   •   3 min

Són les $10\!:\!35$. Quina hora serà d'aquí a $2017$ minuts?
A. $20\!:\!12$
B. $12\!:\!12$
C. $00\!:\!12$
D. $20\!:\!00$
E. $15\!:\!12$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 7
4 punts   •   3 min

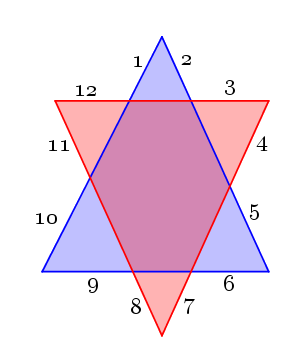
Superposem, de la forma que volem, dos triangles de la nostra tria, i ens fixem en el perímetre exterior del polígon que formen. Quin dels següents polígons segur que no podrem formar?

Per exemple, sí que podem obtindre un dodecàgon:

A. Triangle
B. Quadrilàter
C. Pentàgon
D. Hexàgon
E. Tots els anteriors es poden formar
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 8
4 punts   •   3 min

A quina hora entre les $2$ i les $3$ coincideixen les busques de les hores i dels minuts?
A. $2\!:\!10\!:\!54$
B. $2\!:\!11\!:\!00$
C. $2\!:\!10\!:\!30$
D. $2\!:\!10\!:\!44$
E. $2\!:\!11\!:\!21$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 9
4 punts   •   3 min

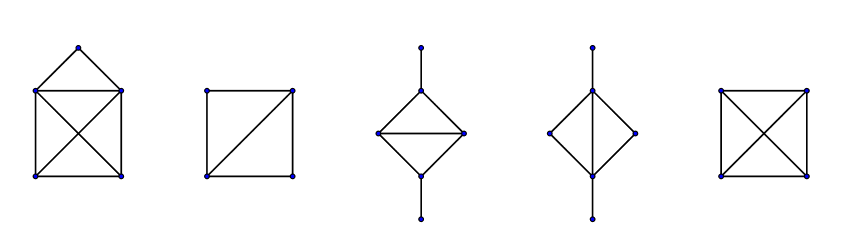
Quantes de les següents figures es poden formar sense alçar el llapis del paper i sense passar dos cops per un mateix segment?

A. $1$
B. $2$
C. $3$
D. $4$
E. $5$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 10
4 punts   •   3 min

A la successió de Fibonacci, cada terme és la suma dels dos anteriors. Comença així: $$1,\ 1,\ 2,\ 3,\ 5,\ \ldots$$ Si ens fixem en la xifra de les unitats dels termes, quin dels deu dígits $(0,1,2,\ldots,9)$ és l'últim que apareix?
A. $6$
B. $5$
C. $0$
D. $7$
E. $9$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 11
5 punts   •   4 min 30 s

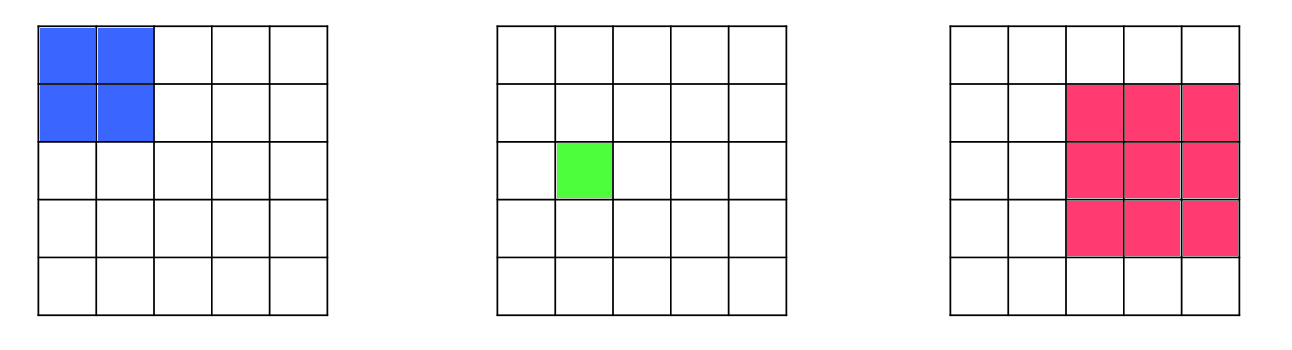
Quants quadrats podem formar amb una quadrícula de $5\times5$?

Els costats dels quadrats han de coincidir amb els segments de la quadrícula. Alguns exemples de quadrats són:

A. $55$
B. $45$
C. $100$
D. $25$
E. $125$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 12
5 punts   •   4 min 30 s

Quina és la suma de les xifres del resultat de multiplicar el número $111\cdots111$ ($2017$ uns), per $2017$?
A. $2017$
B. $2044$
C. $24204$
D. $20170$
E. $1000$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 13
5 punts   •   4 min 30 s

A un triangle equilàter negre li inscrivim un altre triangle equilàter invertit blanc. A aquest triangle blanc, li inscrivim un altre triangle equilàter negre invertit. Repetim el procés fins a l'infinit, com es veu a la figura:

Quina proporció del triangle original està pintada de negre?

A. $\frac34$
B. $\frac45$
C. $\frac56$
D. $\frac78$
E. No es pot determinar
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 14
5 punts   •   4 min 30 s

Un rellotge quadrat està dividit des del centre en $12$ parts. Tots els angles que surten del centre són iguals, tal com veiem a la figura:

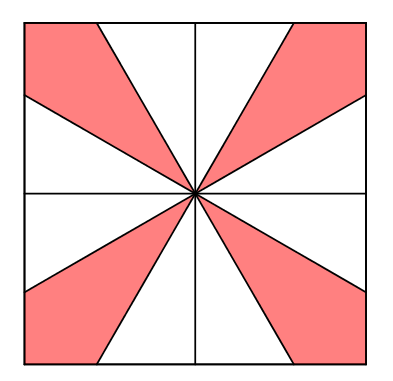
Si l'àrea del quadrat és $1$, quina és l'àrea de la part pintada de vermell?

A. $\frac1{\sqrt3}$
B. $\frac1{\sqrt2}$
C. $1-\frac1{\sqrt2}$
D. $1-\frac1{\sqrt3}$
E. $\frac2{\sqrt3}$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 15
5 punts   •   4 min 30 s

La busca dels minuts i de les hores d'un rellotge se superposen cada $62$ minuts. Quan aquest rellotge marqui el pas d'una hora, quant de temps haurà passat realment?
A. $1\text{ h }$
B. $1\text{ h }2\text{ min}$
C. $56\text{ min }50\text{ s}$
D. $57\text{ min }30\text{ s}$
E. $55\text{ min }40\text{ s}$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Concurs 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat o un curs inferior.

# Usuari Punts Respostes
1. 4t d'ESO  arnaupadres 77
◌
◌
2. 4t d'ESO  Abel 73
◌ ◌
3. 4t d'ESO  PauCantos 69
◌
◌
4. 4t d'ESO  JavierN 67,75
5. 2n de Batxillerat  Al.Chronos 67,25
6. 2n de Batxillerat  javicam 64,5
◌
7. 2n de Batxillerat  ACG_Moià 60,75
8. 4t d'ESO  martijuanola 51,5
◌
◌
9. 4t d'ESO  LuisCasado 49
◌
10. 1r de Batxillerat  selaco_ 47,5
◌
◌
11. 2n de Batxillerat  Monstruhono 45,5
12. 4t d'ESO  Diego123a73 43
◌ ◌ ◌
13. 4t d'ESO  Adri 41,25
14. 1r de Batxillerat  Tumi_1501 39,5
15. 4t d'ESO  capl99 39,25
16. 4t d'ESO  PTallon02 38,75
17. 2n de Batxillerat  AVM_Moià 37,5
18. 2n de Batxillerat  claudiatuneu 35,75
◌
◌ ◌
18. 2n de Batxillerat  Loida 35,75
18. 2n de Batxillerat  LSV_Moià 35,75
◌
21. 2n de Batxillerat  Adrià.LMoià 35
◌
22. 2n de Batxillerat  alcachofa 33,5
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌
23. 2n de Batxillerat  jtorres8_moià 33
24. 2n de Batxillerat  MFC_Moià 30,75
◌ ◌
◌ ◌
◌
25. 1r de Batxillerat  marcmon 28
◌ ◌
◌ ◌ ◌ ◌
◌ ◌ ◌ ◌
25. 2n de Batxillerat  SPMoia 28
◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
27. 2n de Batxillerat  JC 27,25
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌
28. 3r d'ESO  Mireia 27
29. 2n de Batxillerat  AFR_Moià 26
◌
29. 2n de Batxillerat  MGC_Moià 26
31. 2n de Batxillerat  fionasosamoianès 24,75
◌
◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
32. 4t d'ESO  @CatherineLázaro 23,5
◌ ◌ ◌
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌ ◌ ◌

Concurs obert
Usuaris que han superat 2n de Batxillerat, professors, etc.

# Usuari Punts Respostes
1. Professor/a  Rafel_J 72,5
◌
2. Professor/a  rafel 71,25
◌ ◌
3. Professor/a  RamonCanet 44,25
◌ ◌ ◌ ◌

Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.

# Usuari Punts Respostes
1. Universitat  PINSO_PINSO 100
2. Universitat  ikerzr 87
3. Universitat  VíctorConchello 68,5
◌
4. Universitat  PolO 59,5
5. Curs indeterminat  DANIVILARDELL 58,75
◌
6. Universitat  marcof2 55,75

Llegenda

  →   Resposta correcta

  →   Resposta correcta més ràpida de la taula (+1 punt)

  →   Resposta incorrecta