Contrarellotge temàtica: el temps (2n d'ESO)
Dilluns, 9 d’octubre de 2017 a les 19:00

Premi: Taller al Museu de Matemàtiques de Catalunya


El primer classificat a la Contrarellotge guanyarà un val per 4 persones per visitar el Museu de Matemàtiques de Catalunya i realitzar el taller de «Les cúpules de Leonardo».

Entra o registra't per participar al Concurs virtual per reviure aquesta contrarellotge. Se t'aniran plantejant els problemes com el dia del concurs, i a més competiràs contra els participants d'aquell dia: veuràs com van marcant les respostes tal com ho van fer el durant del concurs.

Podràs repetir tants cops com vulgues, i el teu resultat només es farà públic si ho tries així.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Problema 1
3 punts   •   1 min 30 s

Un rellotge digital mostra l'hora i els minuts, des de les $00\!:\!00$ fins les $23\!:\!59$.

Quants minuts al dia el rellotge mostra el mateix dígit repetit $4$ cops?

A. $1$
B. $2$
C. $3$
D. $4$
E. $240$
En blanc
Mostra solució
Només hi ha $3$ minuts en què els quatre dígits són el mateix: $$00\!:\!00$$ $$11\!:\!11$$ $$22\!:\!22$$

Problema 2
3 punts   •   1 min 30 s

És migdia i el rellotge marca les $12$ en punt:

Quina hora marcarà després de $2017$ hores?

A. $1$
B. $3$
C. $5$
D. $7$
E. $9$
En blanc
Mostra solució

Cada $12$ hores, el rellotge torna a marcar la mateixa hora. Per tant, hem d'esbrinar el residu de la divisió per $12$: $$2017=168\cdot12 + 1$$

El residu és $1$ i el rellotge marcarà la una:

Problema 3
3 punts   •   1 min 30 s

Tenim el costum de calcular la suma de les xifres que mostra un rellotge digital. Per exemple, a les $\text{15:33}$ la suma és $1+5+3+3=12$.

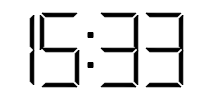
Quina és la suma màxima que podem observar?

A. $20$
B. $22$
C. $23$
D. $24$
E. $25$
En blanc
Mostra solució

Pel que fa als minuts, la xifra de les unitats serà $9$ com a molt i la de les desenes $5$. Com $59$ són uns minuts vàlids, aquest serà el nombre.

Pel que fa a les hores, les unitats seran $9$ com a molt. Les desenes poden ser $0,1,2$, però si són $2$, la suma màxima serà a les $23$ hores. És evident que a les $19$ obtenim una suma major.

Per tant, la suma màxima l'obtenim a les $19\!:\!59$, i és: $$ \text{màxima suma}=1+9+5+9=24 $$

Problema 4
3 punts   •   1 min 30 s

Tenim dos rellotges espatllats. Un s'avança $5$ minuts cada hora, i l'altre es retrassa $5$ minuts cada hora.

Si els posem a hora els dos, quant de temps passarà fins que estiguen desfasats una hora?

A. $1\text{ h}$
B. $5\text{ h}$
C. $4\text{ h}$
D. $6\text{ h}$
E. $8\text{ h}$
En blanc
Mostra solució
Cada hora que passa els rellotges es desfasen $5+5=10\text{ min}$. Per tant, hauran de passar $6\text{ h}$ fins que es desfassin $60\text{ min}$.

Problema 5
3 punts   •   1 min 30 s

Quin nombre de les opcions compleix les següents condicions:

  • No és primer.
  • No és múltiple de $5$.
  • El residu de dividir-lo per $3$ és $1$.
A. $13$
B. $35$
C. $37$
D. $73$
E. $49$
En blanc
Mostra solució
El número $49$ compleix totes les condicions: no és primer $(49=7^2)$, ni múltiple de $5$, i $49=16\cdot3+1$.

Problema 6
4 punts   •   3 min

Siguen $x,y,z$ que compleixen el següent sistema: $$\begin{cases} y&+&y&+&x & =&23\\ y&+&z&+&z & =&10\\ x&+&x&+&x & =&45 \end{cases}$$ Quin és el resultat de la següent expressió? $$z\ +\ y\ +\ xy\ =\ ?$$
A. $62$
B. $54$
C. $34$
D. $67$
E. $73$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 7
4 punts   •   3 min

Un campanar toca els quarts ($1$ campanada al primer quart, $2$ a dos quarts, $3$ als tres quarts i $4$ a l'hora en punt). A més, a l'hora en punt toca tantes campanades com l'hora que és.

Quantes campanades toca al llarg de tot un dia?

A. $198$
B. $256$
C. $312$
D. $356$
E. $396$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 8
4 punts   •   3 min

Pintem de vermell l'àrea entre un cercle de radi $2$ i dos cercles interiors tangents de radi $1$. Quant mesura l'àrea vermella?

A. $1\pi$
B. $2\pi$
C. $3\pi$
D. $2$
E. $4\pi^2$
En blanc
Mostra solució

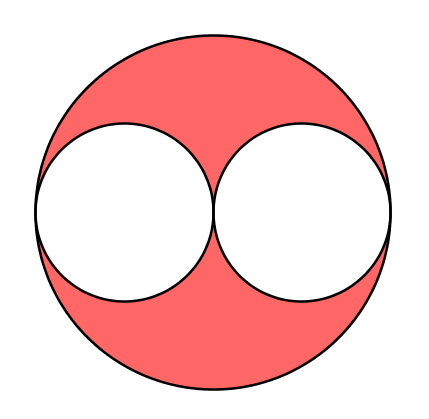
Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 9
4 punts   •   3 min

Un rellotge digital marca les hores entre les $00\!:\!00$ i les $23\!:\!59$. Quants minuts al dia és l'hora capicua?

Per exemple, les $13\!:\!31$ són una hora capicua.

A. $12$
B. $14$
C. $16$
D. $60$
E. $18$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 10
4 punts   •   3 min

Quantes vegades coincideixen les busques de les hores i dels minuts d'un rellotge de paret entre mitjanit i migdia (ambdós moments inclosos)?
A. $10$
B. $11$
C. $12$
D. $13$
E. $14$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 11
5 punts   •   4 min 30 s

Un tronc cilíndric pesa $20\text{ kg}$. Quant pesaria si fóra el doble de gruixut (el doble de diàmetre) i la meitat de llarg?
A. $10 \text{ kg}$
B. $20 \text{ kg}$
C. $30 \text{ kg}$
D. $40 \text{ kg}$
E. $80 \text{ kg}$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 12
5 punts   •   4 min 30 s

Dos nombres sumen $S$. Sumem $2$ a cadascun dels nombres i després els multipliquem per $3$. Quina és la suma dels nombres que hem obtingut?
A. $3S+3$
B. $3S+6$
C. $3S+12$
D. $6S$
E. $2S+6$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 13
5 punts   •   4 min 30 s

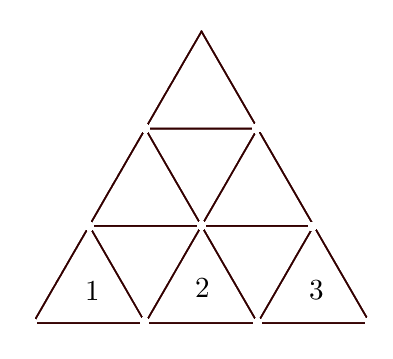Usant furgadents, formem un triangle sobre la taula seguint el següent patró: A la figura anterior, la base té $3$ triangles. Quants furgadents necessitarem en total per fer un triangle amb $2017$ triangles a la base?
A. $6.105.459$
B. $2.035.153$
C. $12.210.918$
D. $4.070.306$
E. $3.000.000$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 14
5 punts   •   4 min 30 s

El meu pare és $4$ vegades més gran que jo, però fa $4$ anys era $6$ vegades més gran. Quants anys tinc?
A. $8$
B. $9$
C. $10$
D. $11$
E. $12$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Problema 15
5 punts   •   4 min 30 s

Quin angle formen les busques d'un rellotge a les $4\!:\!08$?
A. $75^\circ$
B. $76^\circ$
C. $80^\circ$
D. $85^\circ$
E. $90^\circ$
En blanc
Mostra solució

Entra o registra't per consultar les solucions dels problemes del 2n i 3r bloc. Tots els problemes de la Contrarellotge matemàtica inclouen una explicació detallada de la seua resolució.

Concurs 2n d'ESO
Estudiants que cursen 2n d'ESO o un curs inferior.

# Usuari Punts Respostes
1. 2n d'ESO  Alexl 85,75
2. 2n d'ESO  Kolmogorov 74,25
◌
3. 1r d'ESO  asaperas 68
◌
4. 2n d'ESO  visca 66,5
◌
5. 2n d'ESO  AlexNavarrov 64,75
◌ ◌ ◌
6. 2n d'ESO  mmontull 60,25
7. 2n d'ESO  MuFFiN 59,25
◌
8. 2n d'ESO  anubis 56,75
◌
9. 2n d'ESO  mros 54,5
10. 2n d'ESO  nunusevillano 53
11. 1r d'ESO  CarlosBarrosoSellés 52,25
◌
12. 2n d'ESO  Jamer7 52
◌
13. 2n d'ESO  Pauet37 50,75
◌ ◌
14. 2n d'ESO  Núria_04 50,25
15. 2n d'ESO  jaimehedj 44,25
◌ ◌ ◌
◌
16. 2n d'ESO  LaiaMaso13 44
17. 2n d'ESO  Ferran_campmol 41
◌
◌
18. 2n d'ESO  PaulaBosch 40,5
◌
19. 2n d'ESO  judith.bagur 40
20. 2n d'ESO  NúriaG 38,75
21. 2n d'ESO  Nareta347 36
◌ ◌
◌
◌
22. 2n d'ESO  Helena 35,75
23. 1r d'ESO  noeliapc 33,5
◌
24. 2n d'ESO  IonaV 32
◌ ◌ ◌ ◌ ◌
25. 2n d'ESO  Douae+.+ 30,5
◌
26. 2n d'ESO  mireiajuanola 29,25
◌ ◌
◌ ◌ ◌ ◌
◌ ◌ ◌ ◌
27. 2n d'ESO  cristinamartinezc 28
28. 2n d'ESO  abrilgarcia2nB 27
29. 2n d'ESO  felipecampos 25,5
◌ ◌ ◌ ◌ ◌
◌ ◌ ◌
◌ ◌ ◌
30. 2n d'ESO  areej.868 14,75

Concurs obert
Usuaris que han superat 2n d'ESO, professors, etc.

# Usuari Punts Respostes
1. Professor/a  Frederic 82,25
2. Professor/a  JMB 77
3. 4t d'ESO  martijuanola 75,5
4. 1r de Batxillerat  enriquervwtf 73
5. 4t d'ESO  JPG 66,75
◌
6. 1r d'ESO  Pablo 61,75
7. Professor/a  Mcorb 61
◌ ◌ ◌
8. 4t d'ESO  Ssr 53
◌ ◌
9. 4t d'ESO  Diego123a73 51,75
◌ ◌ ◌ ◌ ◌
◌
◌
10. 4t d'ESO  Ivet_R 43,75
11. 4t d'ESO  doonald_12 39
12. 1r de Batxillerat  marcmon 33
◌ ◌
◌ ◌ ◌
◌ ◌

Concurs virtual
Usuaris que han participat al Concurs virtual, un cop acabada la prova.

# Usuari Punts Respostes
1. Universitat  Diego123a73 100
1. Universitat  doonald_12 100
1. Curs indeterminat  JoanAn 100
1. 1r d'ESO  JUANMA05@madina 100
1. Universitat  Núria_04 100
6. Universitat  Joel5ln 99
7. Universitat  J.P.B 94
8. Universitat  Marti 91,75
9. Universitat  gretathunberg 91
10. Curs indeterminat  alejsales 88
◌
10. Universitat  arnaupadres 88
12. Universitat  Lettypozo 87
◌
13. 1r d'ESO  ClaraMas@madina 86,75
14. Universitat  joanbr 82
15. Universitat  Bibiana_Aina 81,5
16. Universitat  a 80,75
17. Universitat  Snopah 79,75
18. Universitat  ikerzr 73,75
19. Universitat  laiagc 73
◌
20. Curs indeterminat  ErikF 72,75
21. Universitat  Euler 70,5
◌
◌
22. Curs indeterminat  Caarlaa 68,5
23. Universitat  Thaïs 67,75
24. Universitat  nadia.R.L 64,75
25. Universitat  Laura-Andreu 64,5
26. Universitat  DiegoT 62,75
27. Universitat  txellcj 60,5
28. Universitat  ruben_42i 59,25
◌
◌
29. Universitat  polgm 58,25
30. Universitat  jaumeam 56
◌
◌ ◌ ◌
31. Universitat  Marc_Gili 55,75
32. 1r d'ESO  IKER13@MADINA 53,25
◌
◌
33. Universitat  Clara_Romo 52,25
34. Universitat  polbm 51
35. 1r d'ESO  Blaideesteban6@madina 49,75
36. 1r d'ESO  júliaandrésmatesmadina 45,75
37. Universitat  Marta09 45
38. Universitat  Al3x15 44,25
◌
◌ ◌ ◌ ◌ ◌
39. 1r d'ESO  ainapau@madina 40,25
39. Universitat  Anna 40,25
◌
41. Curs indeterminat  Mireieta 38,5
42. Universitat  IGN_Moià 38,25
43. 1r d'ESO  Rafelbusaribatard@madina 36,75
44. 2n de Batxillerat  megawarret3000 34,25
45. Universitat  Jorge 31,5
◌
45. Curs indeterminat  P 31,5
◌
47. 1r d'ESO  Paulosky9Fajardo@madina 30,5
◌
48. Universitat  Guillem.C.M 29,25
◌ ◌
◌
49. Universitat  Marta 20,75

Llegenda

  →   Resposta correcta

  →   Resposta correcta més ràpida de la taula (+1 punt)

  →   Resposta incorrecta