En un triangle equilàter, hi encabim tres quadrats tal com s'indica a la figura, i els costats dels quadrats són $l, 2l$ i $3l$ per a un cert $l$ real positiu.
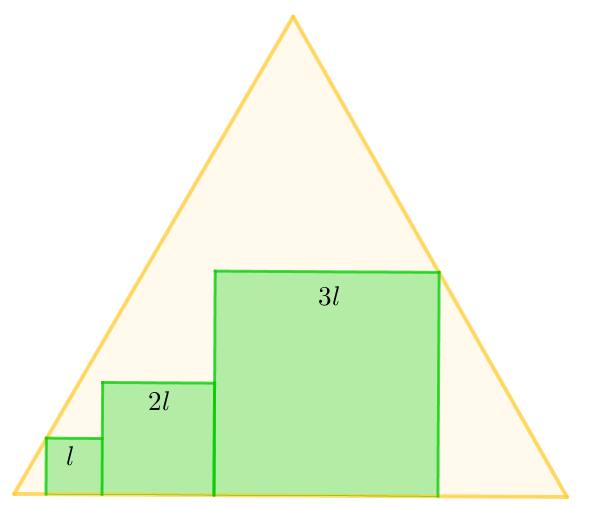
Calculem la divisió: $\dfrac{\text{àrea total del triangle equilàter}}{\text{àrea dels quadrats}}$ i l'expressem en la forma $\dfrac{a+b\sqrt{3}}{c}$ (amb $a,b,c$ naturals sense cap factor comú). Quant val $b$?
Primer de tot trobarem la longitud del costat del triangle equilàter. Per a això, notem que en els dos triangles que ens apareixen als costats dels quadrats tenen angles $30^{\circ} - 60^{\circ} - 90^{\circ}$
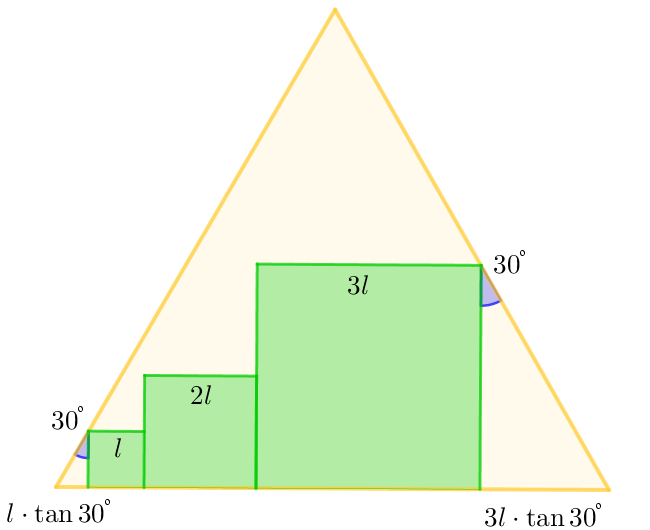
En particular, amb un càlcul senzill de trigonometria podem trobar la longitud dels segments que desconeixem. En total, la base del triangle fa $$ l \tan 30^\circ + l + 2l + 3l + 3l \tan 30^\circ = l \Big(6 + \frac{4}{\sqrt{3}} \Big) $$
L'àrea dels quadrats és senzilla de calcular $$ l^2 + (2l)^2 + (3l)^2 $$
L'àrea d'un triangle equilàter de costat $c$ és $\frac{c^2\sqrt{3}}{4}$, substituint la longitud del costat que acabem de trobar tenim que l'àrea del triangle és $$\frac{ l^2 \big(6 + \frac{4}{\sqrt{3}} \big)^2 \sqrt{3}}{4} $$
Entra o registra't per consultar les solucions dels Problemes del mes de 4t d'ESO i 2n de batxillerat.
Classificació 2n de Batxillerat
Estudiants que cursen 2n de Batxillerat
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | lorodane | lorodane | 1 d’octubre de 2020 a les 8:20 | 01/10/2020 |
| Or | Nomarolbap | Nomarolbap | 1 d’octubre de 2020 a les 9:41 | 01/10/2020 |
| Or | ÀlexRodríguez | ÀlexRodríguez | 2 d’octubre de 2020 a les 16:42 | 02/10/2020 |
| Or | enriccat | enriccat | 2 d’octubre de 2020 a les 17:31 | 02/10/2020 |
| Or | visca | visca | 2 d’octubre de 2020 a les 20:29 | 02/10/2020 |
| Or | PolPifa | PolPifa | 4 d’octubre de 2020 a les 0:19 | 04/10/2020 |
| Or | lriuet | lriuet | 5 d’octubre de 2020 a les 10:05 | 05/10/2020 |
| Or | alfonsopas... | alfonsopastor__ | 5 d’octubre de 2020 a les 13:20 | 05/10/2020 |
| Or | Alexia2005 | Alexia2005 | 5 d’octubre de 2020 a les 18:28 | 05/10/2020 |
| Or | arnoldfini | arnoldfini | 5 d’octubre de 2020 a les 21:56 | 05/10/2020 |
| Or | rbargallor | rbargallor | 24 d’octubre de 2020 a les 17:15 | 24/10/2020 |
| Plata | nailabernaus | nailabernaus | 5 d’octubre de 2020 a les 0:28 | 05/10/2020 |
| Plata | CXZ03 | CXZ03 | 21 d’octubre de 2020 a les 21:56 | 21/10/2020 |
| Plata | PauMB | PauMB | 24 d’octubre de 2020 a les 17:15 | 24/10/2020 |
| Plata | martinos | martinos | 31 d’octubre de 2020 a les 14:24 | 31/10/2020 |
| Bronze | Farrius | Farrius | 1 d’octubre de 2020 a les 20:13 | 01/10/2020 |
| Bronze | Núria_04 | Núria_04 | 6 d’octubre de 2020 a les 20:49 | 06/10/2020 |
| Bronze | lauvilo | lauvilo | 31 d’octubre de 2020 a les 17:54 | 31/10/2020 |
| Xocolata | paulavidal | paulavidal | 4 d’octubre de 2020 a les 12:26 | 04/10/2020 |
| Xocolata | crissana | crissana | 21 d’octubre de 2020 a les 23:22 | 21/10/2020 |
| Xocolata | Bernat | Bernat | 24 d’octubre de 2020 a les 20:08 | 24/10/2020 |
| Xocolata | PolO | PolO | 27 d’octubre de 2020 a les 20:39 | 27/10/2020 |
Classificació oberta
Usuaris que ja han superat
2n de Batxillerat.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | Sergi_bm | Sergi_bm | 1 d’octubre de 2020 a les 8:48 | 01/10/2020 |
| Or | rsempere | rsempere | 1 d’octubre de 2020 a les 10:47 | 01/10/2020 |
| Or | montserrat... | montserrat.muria | 1 d’octubre de 2020 a les 18:05 | 01/10/2020 |
| Or | bach22 | bach22 | 2 d’octubre de 2020 a les 18:25 | 02/10/2020 |
| Or | JABorrás | JABorrás | 2 d’octubre de 2020 a les 21:23 | 02/10/2020 |
| Or | joanmatematic | joanmatematic | 3 d’octubre de 2020 a les 17:34 | 03/10/2020 |
| Or | AlexKende | AlexKende | 4 d’octubre de 2020 a les 13:43 | 04/10/2020 |
| Or | arakelov | arakelov | 24 d’octubre de 2020 a les 8:36 | 24/10/2020 |
| Plata | JM | JM | 1 d’octubre de 2020 a les 8:16 | 01/10/2020 |
| Plata | BMartinell | BMartinell | 2 d’octubre de 2020 a les 15:10 | 02/10/2020 |
| Plata | PauCantos | PauCantos | 4 d’octubre de 2020 a les 0:01 | 04/10/2020 |
| Plata | avelez6 | avelez6 | 25 d’octubre de 2020 a les 11:24 | 25/10/2020 |
| Bronze | ZHENO | ZHENO | 21 d’octubre de 2020 a les 19:24 | 21/10/2020 |
