Sabent que l'àrea del quadrat blau és $100$, calcula l'àrea de la creu inscrita en el cercle:
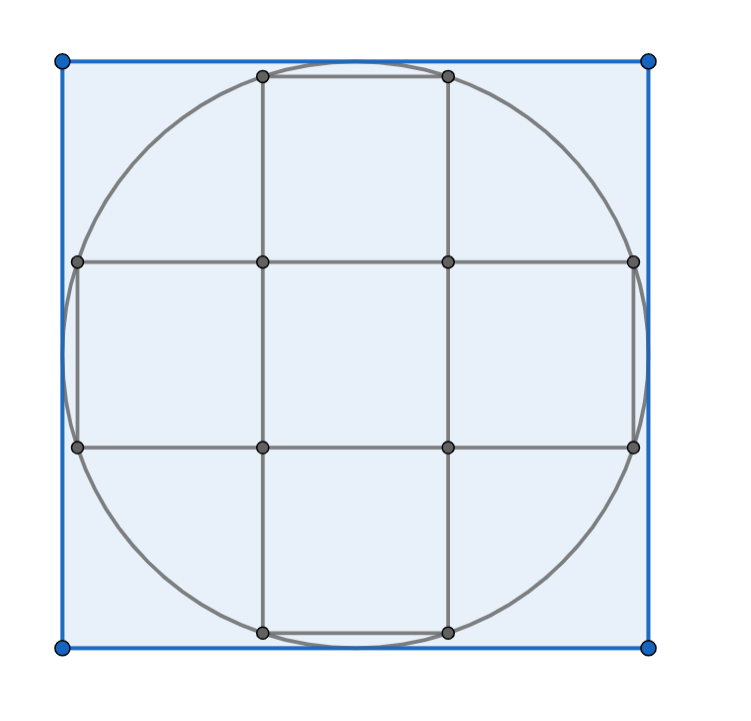
Ens cal trobar el costat dels quadrats petits que formen la creu. Per això farem Pitàgores amb un triangle rectangle que combini el costat d'un quadrat petit amb el radi del cercle.Tingueu en compte que tota la figura té simetria respecte al centre del cercle. Per tant, el centre i el radi sòn claus per construir el triangle rectangle apropiat. Intenta buscar aquest triangle rectangle.
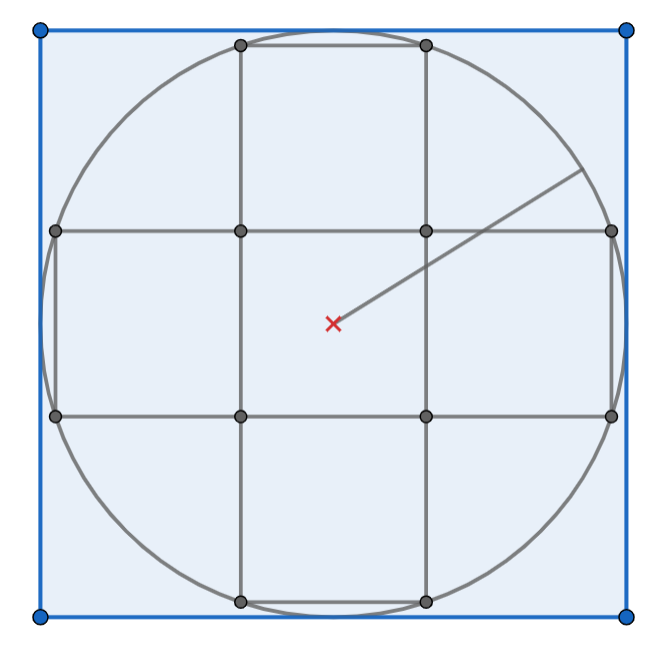
El triangle rectangle és el següent:
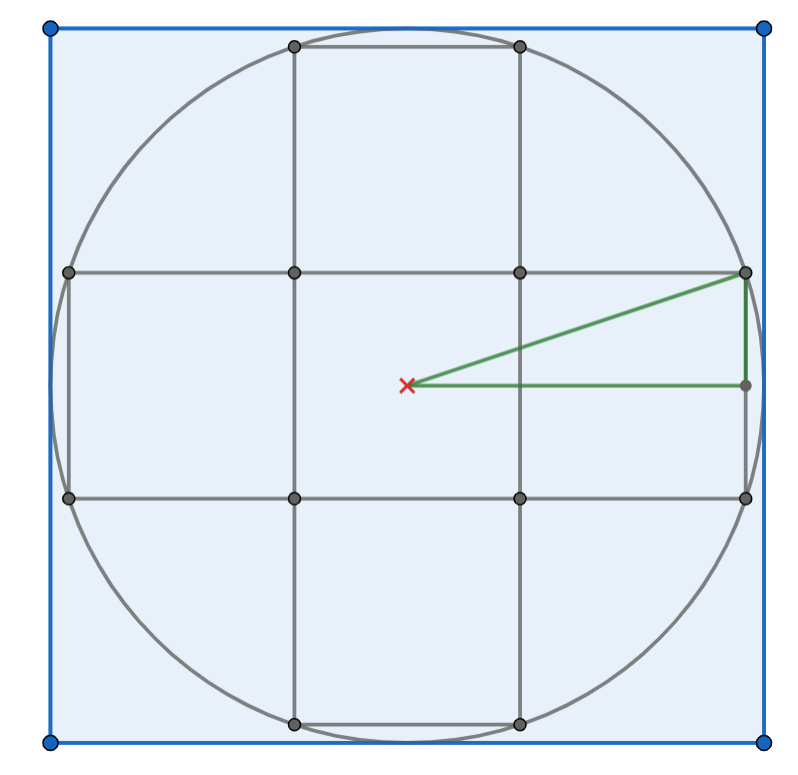
Sabem que el costat del quadrat gran és $10$, per tant el radi del cercle és $R=5$. Escrivim l'equació en funció de $l$, de manera que els catets del triangle rectangle són $l/2, 3l/2$. El Pitàgores que hem fet ens diu que: $$ R^2 = \left(\frac{l}{2}\right)^2 + \left(\frac{3l}{2}\right)^2$$
Per tant tenim que $l^2 = \frac{2}{5}R^2$. Per tant, $l^2 = 10$. Amb això ja tenim l'área de la creu.
Considerem un triangle rectangle construit sobre el centre del cercle.

Sigui $R$ el radi del cercle i sigui $l$ el costat d'un quadrat petit. Aleshores tenim que: $$ R^2 = \left(\frac{l}{2}\right)^2 + \left(\frac{3l}{2}\right)^2$$
$R$ és la meitat del costat del quadrat gran, per tant $R=5$. Per l'equació de Pitàgores tenim $l^2 = 2R^2/5 = 10$. Per tant, l'àrea total és $5l^2 = 5\cdot 10 = \boxed{50}$.
Classificació 2n d'ESO
Estudiants que cursen 2n d'ESO
o un curs inferior.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | ian.anderson | ian.anderson | 2 de desembre de 2024 a les 9:29 | 02/12/2024 |
| Or | diego.bosch | diego.bosch | 2 de desembre de 2024 a les 9:49 | 02/12/2024 |
| Or | TomeuAndreu | TomeuAndreu | 2 de desembre de 2024 a les 16:25 | 02/12/2024 |
| Or | lluc.AG | lluc.AG | 2 de desembre de 2024 a les 19:39 | 02/12/2024 |
| Or | I.Toral | I.Toral | 12 de desembre de 2024 a les 12:50 | 12/12/2024 |
| Or | Francesca.... | Francesca.Cesaratto | 13 de desembre de 2024 a les 10:32 | 13/12/2024 |
| Plata | Jorge.barr... | Jorge.barroso.seijas | 2 de desembre de 2024 a les 9:34 | 02/12/2024 |
| Plata | samue690 | samue690 | 2 de desembre de 2024 a les 9:43 | 02/12/2024 |
| Bronze | iago.seoane | iago.seoane | 2 de desembre de 2024 a les 9:42 | 02/12/2024 |
| Bronze | E.GrechMayans | E.GrechMayans | 2 de desembre de 2024 a les 10:55 | 02/12/2024 |
Classificació oberta
Usuaris que ja han superat
2n d'ESO.
| Medalla | # | Usuari | Data | |
|---|---|---|---|---|
| Or | Pep123 | Pep123 | 1 de desembre de 2024 a les 21:49 | 01/12/2024 |
| Or | Pedro | Pedro | 2 de desembre de 2024 a les 9:33 | 02/12/2024 |
| Or | Tanis | Tanis | 2 de desembre de 2024 a les 9:35 | 02/12/2024 |
| Or | Santiago | Santiago | 2 de desembre de 2024 a les 15:18 | 02/12/2024 |
| Or | arakelov | arakelov | 6 de desembre de 2024 a les 16:49 | 06/12/2024 |
